Hypothesis testing
<slideshow style="nobleprog" headingmark="。" incmark="…" scaled="false" font="Trebuchet MS" >
- title
- Hypothesis Testing
</slideshow> Prerequisites
Hypothesis Testing。
- Usages
- Checking the probability of things being different
- Examples
- Is the new version of software better than the previous one?
- Do women watch YouTube more often than man?
- Does blue background of the background makes people less tired than red one?
Questions。
- How can we distinguish between two things?
- What is the probability that the conclusion is not due to pure chance?
- What is a difference between:
- Probability of an event
- Probability of a state of the world
- How to define the "null hypothesis" and the "alternative hypothesis"
Lady Tasting Tea。


Ronald Fisher explained the concept of hypothesis testing with a story of a lady tasting tea.
- The lady in question claimed to be able to tell whether the tea or the milk was added first to a cup.
- Fisher gave her eight cups, four of each variety, in random order.
- The woman got all eight cups correct.
- What is the probability that she got it right, but just by pure chance?
Answer。
Answer >>
- There is 1 in 70 (the combinations of 8 taken 4 at a time) chance that if she couldn't tell the difference, should would guess all 8 cups
- This is 1.4% significance level, below normally assumed 5%
- More on Wikipedia.
James Bond Example。

Problem
- James Bond insists that Martinis should be shaken rather than stirred
- We want to determine whether Mr. Bond can tell the difference between a shaken and a stirred Martini
Experiment
- Suppose we gave Mr. Bond a series of 16 taste tests
- In each test, we flipped a fair coin to determine whether to stir or shake the Martini
- Then we presented the martini to Mr. Bond and asked him to decide whether it was shaken or stirred
Results
- Let's say Mr. Bond was correct on 13 of the 16 taste tests
- Can he tell the difference?
Interpretation
- This result does not prove that he does!
- It could be he was just lucky and guessed right 13 out of 16 times
- How plausible is the explanation that he was just lucky?
Answer。
Answer >>
- To assess its plausibility, we determine the probability that someone who was just guessing would be correct 13/16 times or more
- This probability can be computed from the binomial distribution
- http://www.stat.tamu.edu/~west/applets/binomialdemo.html
- Google Cal:
- 1-binomdist(12,16,0.5,true)
- binomdist(13,16,0.5,false)+binomdist(14,16,0.5,false)+binomdist(15,16,0.5,false) +binomdist(16,16,0.5,false)
- Binomial distribution calculator shows it to be 0.0106
- He could have guessed it once in every hundred trials
- So either Mr. Bond was very lucky, or he can tell whether the drink was shaken or stirred
- The hypothesis that he was guessing is not proven false, but considerable doubt is cast on it
- Therefore, there is strong evidence that Mr. Bond can tell whether a drink was shaken or stirred
Physicians' Reactions。

Problem
- Do physicians spend less time with obese patients?
Experiment
- Physicians were sampled randomly and each was shown a chart of a patient complaining of a migraine headache
- They were then asked to estimate how long they would spend with the patient
- The charts were identical except that for half the charts, the patient was obese and for the other half, the patient was of normal weight
- The chart a particular physician viewed was determined randomly
- 31 physicians viewed charts of average-weight patients and 38 physicians viewed charts of obese patients
Results
- The reported mean time spend with patients:
- obese 24.7min
- average-weight: 31.4min
- How might this difference between means have occurred?
Interpretation。
Answer >>
- Two possibilities:
- physicians were influenced by the weight of the patients
- by pure chance
- Random assignment of charts does not ensure that the groups will be equal in all respects other than the chart they viewed
- In fact, it is certain the groups differed in many ways by chance (e.g. mean age, gender, race, etc...)
- How possible it is that these chance differences are responsible for the difference in times?
- What is the probability of getting a difference as large or larger than the observed difference (6.7min) due to chance?
- This probability can be computed to be 0.0057 (one in 175 experiments) - see Differences between Two Means (Independent Groups)
- Since this is a low probability, we have confidence that the difference in times is due to the patient's weight and is not due to chance
The Probability Value。
- Probability value is also know as "P", "P-value" or "p"
- In the James Bond example, the computed probability of 0.0106 is the probability he would be correct on 13 or more taste tests (out of 16) if he were just guessing (i.e. by pure chance).
- The 0.0106 is NOT the probability he cannot tell the difference
- The probability of 0.016 is the probability of a certain outcome (13 or more out of 16) assuming a certain state of the world (James Bond was only guessing.)
- It is not the probability that a state of world is true
An example - a bird which knows how to divide。

- An animal trainer claims that a trained bird can determine whether or not numbers are evenly divisible by 7
- In an experiment assessing this claim, the bird is given a series of 16 test trials
- On each trial, a number is displayed on a screen and the bird pecks at one of two keys to indicate its choice
- The numbers are chosen in such a way that the probability of any number being evenly divisible by 7 is 0.50
- The bird is correct on 9/16 choices
Answer。
Answer >>
- From binomial distribution, the probability of being correct nine or more times out of 16 if one is only guessing is 0.40
- Since a bird who is only guessing would do this well 40% of the time, these data do not provide convincing evidence that the bird can tell the difference between the two types of numbers
- The 40% does NOT mean that there is a 0.40 probability that the bird can tell the difference!!!
- The probability value is the probability of an outcome (9/16 or better) and not the probability of a particular state of the world (the bird can tell whether a number is divisible by 7)
State of the world vs an outcome。
- Hypotheses are The possible states of the world
- The probability value is the probability of an outcome given the hypothesis
- It is not the probability of the hypothesis given the outcome
- If the probability of the outcome given the hypothesis is sufficiently low, we have evidence that the hypothesis false
- However, we do not compute the probability that the hypothesis is false
- In the James Bond example, the hypothesis is that he cannot tell the difference between shaken and stirred martinis
- The probability value is low (0.0106), thus providing evidence that he can tell the difference
- However, we have not computed the probability that he can tell the difference
- A branch of statistics called Bayesian statistics provides methods for computing the probabilities of hypotheses
The Null Hypothesis。
- The null hypothesis is that an apparent effect is due to chance
In the Physicians' Reactions example, the null hypothesis is that in the population of physicians, the mean time expected to be spent with obese patients is equal to the mean time expected to be spent with average-weight patients:
H0: μobese = μaverage or H0: μobese - μaverage = 0.
In a correlational study of the relationship between high-school grades and college grades would be that the population correlation is 0
H0: ρ = 0
The test for a biased coin:
H0: π = 0.5
- The null hypothesis is typically the opposite of the researcher's hypothesis
- the physicians were expect to spend less time with obese patients, but the null hypothesis is they do not.
- ff the null hypothesis were true, a difference as large or larger than the sample difference of 6.7 minutes would be very unlikely to occur
- therefore, the researchers rejected the null hypothesis of no difference and concluded that in the population, physicians intend to spend less time with obese patients
The alternative hypothesis。
- If the null hypothesis is rejected, then the alternative hypothesis is accepted
- The alternative hypothesis is simply the reverse of the null hypothesis
H0: μobese = μaverage is rejected, then there are two alternatives: H1: μobese < μaverage or H1: μobese > μaverage
- The direction of the sample means determines which alternative is adopted
Questions。
Please do the questions on the website (not in presentation mode)
Questions
Template:Statistics Links
Hypothesis Testing | Significance Testing >
Significance Testing
Questions
- How a probability value is used to cast doubt on the null hypothesis?
- What does the phrase "statistically significant" mean
- What is a difference between statistical significance and practical significance
- What are the two approaches significance testing
Significance level
- A low probability value casts doubt on the null hypothesis
- How low must the probability value be in order to conclude that the null hypothesis is false?
- there is clearly no right or wrong answer
- p < 0.05
- p < 0.01
- When a researcher concludes that the null hypothesis is false, the researcher is said to have rejected the null hypothesis
- The probability value below which the null hypothesis is rejected is called significance level or α level or simply α
Statistical significance vs. practical significance
- When the null hypothesis is rejected, the effect is said to be statistically significant
- For example, in the Physicians Reactions case study, the p-value is 0.0057
- Therefore, the effect of obesity is statistically significant and the null hypothesis that obesity makes no difference is rejected
- It is very important to keep in mind that statistical significance means only that the null hypothesis of exactly no effect is rejected; it does not mean that the effect is important, which is what "significant" usually means
- When an effect is significant, you can have confidence the effect is not exactly zero
- Finding that an effect is significant does not tell you about how large or important the effect is.
Do not confuse statistical significance with practical significance. A small effect can be highly significant if the sample size is large enough.
Why does the word "significant" in the phrase "statistically significant" mean something so different from other uses of the word?
Answer >>
- The meaning of "significant" in everyday language has changed
- In the 19th century, something was "significant" if it signified something
- Finding that an effect is statistically significant signifies that the effect is real and not due to chance
- Over the years, the meaning of "significant" changed, leading to the potential misinterpretation.
Two approaches to conducting significance tests
Ronald Fisher Approach
- A significance test is conducted and the probability value reflects the strength of the evidence against the null hypothesis
| P-values | Meaning |
|---|---|
| below 0.01 | the data provide strong evidence that the null hypothesis is false |
| between 0.01 and 0.05 | the null hypothesis is typically rejected, but not with less confidence |
| between 0.05 and 0.10 | provide weak evidence against the null hypothesis, are not considered low enough to justify rejecting it |
Higher probabilities provide less evidence that the null hypothesis is false.
Neyman and Pearson
- An α level is specified before analyzing the data
| P-value | Null Hypothesis |
|---|---|
| P-value < α | H0 is rejected |
| P-value > α | H0 is not rejected |
- If a result is significant, then it does not matter how significant it is
- If it is not significant, then it does not matter how close to being significant it is
- E.g. if α = 0.05 then P-values of 0.049 and 0.001 are treated identically
- Similarly, probability values of 0.06 and 0.34 are treated identically
Comparison of approaches
The Fisher approach is more suitable for scientific research
- use where there is no need for an immediate decision, e.g. a researcher may conclude that there is some evidence against the null hypothesis
- more research is needed before a definitive conclusion can be drawn
The Pearson is more suitable for applications in which a yes/no decision must be made
- use if you are less interested in assessing the weight of the evidence than knowing what action should be taken
- e.g. should the machine be shut down for repair?
Questions
Template:Statistics Links < Introduction to Hypothesis Testing | Type I and II Errors >
Type I and II Errors
Questions。
- What is Type I and Type II errors?
- How to interpret significant and non-significant differences?
- Why the null hypothesis should not be rejected when the effect is not significant?
Simplification
- Let us assume that null hypothesis is always about something being not different
- E.g.
- new application is as popular as old one (there is not difference in popularity)
- new hardware is as fast as old one (there is no difference in speed)
- drug doesn't cure the disease (makes no difference to patient health)
Overview。
| State of the world | There is no difference | There is a difference |
|---|---|---|
| Null hypothesis (no difference) | Rejected (there is a difference) |
Not Rejected (there is no difference) |
| Error | Type I False Alarm False Positive |
Type II Missed Detection False Negative |
Example 1。
- Patient have a disease
- There is a problem
| State of the world | Patient doesn't have cancer | Patient have cancer |
|---|---|---|
| What we tell the patient | has cancer (H0 rejected) |
no cancer (H0 not rejected) |
| Error | Type I False Alarm False Positive |
Type II Missed Detection False Negative |
Example 2。
- New hardware is different than old one
- Customer is more satisfied with new application than old one
- There is a increase in people buying our product after running Ad-words campaign
| State of the world | No difference between new and old (no difference) | There is a between old and new(difference) |
|---|---|---|
| Null hypothesis (no difference) | Rejected (difference) | Not Rejected (no difference) |
| Error | Type I False detection |
Type II Missed Detection |
Supplier vs Customer
Type I error。
- Type I error is a rejection of a true null hypothesis
- False Positive or False Alarm can be used instead in business world
- Rejecting the null hypothesis is not an all-or-nothing decision
- The Type I error rate is affected by the α level: the lower the α level the lower the Type I error rate
Probability of Type I error。
- It might seem that α is the probability of a Type I error
- However, this is not correct
- Instead, α is the probability of a Type I error given that the null hypothesis is true
You can only make a Type I error if the null hypothesis is true.
Type II error。
- Type II error is failing to reject a false null hypothesis
- Unlike a Type I error, a Type II error is not really an error
- When a statistical test is not significant, it means that the data do not provide strong evidence that the null hypothesis is false
Lack of significance does not support the conclusion that the null hypothesis is true
- Therefore, a researcher would not make the mistake of incorrectly concluding that the null hypothesis is true when a statistical test was not significant
- Instead, the researcher would consider the test inconclusive
- Contrast this with a Type I error in which the researcher erroneously concludes that the null hypothesis is false when, in fact, it is true.
A Type II error can only occur if the null hypothesis is false
- If the null hypothesis is false, then the probability of a Type II error is called β
- The probability of correctly rejecting a false null hypothesis equals 1- β and is called Power
- Power is the probability of being able to find a difference if it really exists
Errors and Decision Making。
- Increasing the significance level, increases the changes of False Alarm and decrease the changes of Miss Detection
- To decrease changes of both errors, the sample size has be increased
What is more serious?。
- False Alarm is usually more serious, as the test is inconclusive
- Missed Detection usually is less harmful e.g.
- if patient failed to detected a disease, they can repeat the test
- on the other hand, if the therapy was implemented to a misdiagnosed problem, the consequence can be worse
- When selecting alpha level which related to probability of False Alarm, it is important to keep that in mind what is more harmful:
- If the administering treatment even for a healthy patient is consider cheap and not harmful, but not detecting the disease of sick patient would be dangerous setting significance level (alpha) high (e.g. 5%) is right thing to do
Supplier v Customer。
- We cannot calculate the probability of Type II error without knowing the true state of the world
- Reduction in probability of Type I error will increase the chance of Type II error
Google v Hard Drive provider
- Hard-drives are provided to the cloud by Company X (supplier) to Google
- H0 is the all hard drives have specification as provided by the supplier
- In other words, the hard drives Google buys, was drawn from the population of the hard drives complying with the spec
- Google tests a sample of the hard drives and test whether they are compliant using Hypothesis Testing
- If Type I error occurs, it is to the suppliers detriment, since hard drives are fine, but will be rejected by Google (after testing)
- If Type II error occurs, Google accepts drives which are not up to the standard
- The sample size can be increased, but that will increase the cost of testing as well
- There is a trade-off between the reduction of errors and the cost of sampling
Supplier v Customer Solution。
- Google and Company X (supplier) can set up alpha and beta to the level where the probability of both errors is the same
- This can be achieved by changing the sample size (sometimes decreasing it), and changing significance level (alpha)
Questions
One-and-Two tailed test
Questions
- When to use one-tailed and when two-tailed test?
One-tailed probability
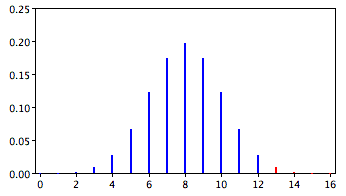
- In the James Bond case study, Mr. Bond was given 16 trials on which he judged whether a martini had been shaken or stirred
- He was correct on 13 of the trials
- From the binomial distribution, we know that the probability of being correct 13 or more times out of 16 if one is only guessing is 0.0106
- The red bars show the values greater than or equal to 13
- As you can see in the figure, the probabilities are calculated for the upper tail of the distribution
- A probability calculated in only one tail of the distribution is called a one-tailed probability
Two-tailed probability
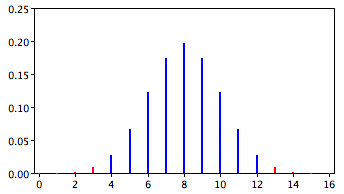
- A slightly different question can be asked of the data: "What is the probability of getting a result as extreme or more extreme than the one observed"?
- Since the chance expectation is 8/16, a result of 3/16 is equally as extreme as 13/16
- Thus, to calculate this probability, we would consider both tails of the distribution
- Since the binomial distribution is symmetric when π = 0.5, this probability is exactly double the probability of 0.0106 computed previously
- Therefore, p = 0.0212
- A probability calculated in both tails of a distribution is called a two-tailed probability
One-tailed vs Two-tailed
Should the one-tailed or the two-tailed probability be used to assess Mr. Bond's performance? That depends on the way the question is posed:
One-tailed
- Is Mr. Bond is better than chance at determining whether a Martini is shaken or stirred?
H0: π ≤ 0.5 H1: π ≥ 0.5 H0 rejected only if the sample proportion is much greater than 0.50.
What would the one-tailed probability be if Mr. Bond was correct on only three of the sixteen trials?
- Since the one-tailed probability is the probability of the right-hand tail, it would be the probability of getting three or more correct out of 16.
- This is a very high probability and the null hypothesis would not be rejected.
Two-tailed
- Can Mr. Bondn tell the difference between shaken or stirred martinis?
- We would conclude he could tell the difference if:
- he performed either much better than chance
- or much worse than chance
- If he performed much worse than chance, we would conclude that he can tell the difference, but he does not know which is which
- Therefore, since we are going to reject the null hypothesis if Mr. Bond does either very well or very poorly, we will use a two-tailed probability
H0: π = 0.5 H1: π ≠ 0.5 H0 rejected if the sample proportion correct deviates greatly from 0.5 in either direction
How to decide?
- You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data
- Tests that compute one-tailed probabilities are called one-tailed tests; those that compute two-tailed probabilities are called two-tailed tests
| One-tailed tests | Two-tailed tests |
|---|---|
| more common in scientific research because an outcome signifying that something other than chance is operating is usually worth noting | appropriate when it is not important to distinguish between no effect and an effect in the unexpected direction |
| Questions like: is A better than B | Questions like: is A has a different effect than B |
Common Cold Treatment
- For example, consider an experiment designed to test the efficacy of treatment for the common cold
- The researcher would only be interested in whether the treatment was better than a placebo control.
- It would not be worth distinguishing between the case in which the treatment was worse than a placebo and the case in which it was the same because in both cases the drug would be worthless
- Even if the researcher predicts the direction of an effect, the two-tailed test might be more appropriate
- If the effect comes out strongly in the non-predicted direction, the researcher is not justified in concluding that the effect is not zero
- Since this is unrealistic, one-tailed tests are usually viewed skeptically if justified on this basis alone.
Questions
Template:Statistics Links < Type I and II Errors | Significant Results >
Interpreting significant results
Questions
- Should rejection of the null hypothesis should be an all-or-none proposition?
- What is the value of a significance test when it is extremely likely that the null hypothesis of no difference is false even before doing the experiment?
Interpreting Significant Results
- When a probability value is below the α level, the effect is statistically significant and the null hypothesis is rejected
- However, not all statistically significant effects should be treated the same way
- For example, you should have less confidence that the null hypothesis is false if p = 0.049 than p = 0.003
- Thus, rejecting the null hypothesis is not an all-or-none proposition
If the null hypothesis is rejected, then the alternative hypothesis is accepted
Interpreting results of one-tailed test
Consider the one-tailed test in the James Bond case study:
- Mr. Bond was given 16 trials on which he judged whether a Martini had been shaken or stirred and the question is whether he is better than chance on this task
H 0 π ≤ 0.5 π is the probability of being correct on any given trial
- If this null hypothesis is rejected, then the alternative hypothesis that π > 0.5 is accepted
- If π is greater than 0.50 then Mr. Bond is better than chance on this task
Interpreting results of two-tailed test
Now consider the two-tailed test used in the Physicians' Reactions case study
H0: μobese = μaverage H1: μobese < μaverage or H1: μobese > μaverage
- The direction of the sample means determines which alternative is adopted
- If the sample mean for the obese patients is significantly lower than the sample mean for the average-weight patients, then one should conclude that the population mean for the obese patients is lower than than the sample mean for the average-weight patients
- There are many situations in which it is very unlikely two conditions will have exactly the same population means
- For example, it is practically impossible that aspirin and acetaminophen provide exactly the same degree of pain relief
- Therefore, even before an experiment comparing their effectiveness is conducted, the researcher knows that the null hypothesis of exactly no difference is false
- However, the researcher does not know which drug offers more relief
- If a test of the difference is significant, then the direction of the difference is established
Can we really tell which population mean is larger?
This text is optional
- Some textbooks have incorrectly stated that rejecting the null hypothesis that two population means are equal does not justify a conclusion about which population mean is larger
- Instead, they say that all one can conclude is that the population means differ
- The validity of concluding the direction of the effect is clear if you note that a two-tailed test at the 0.05 level is equivalent to two separate one-tailed tests each at the 0.025 level
- The two null hypotheses are then
μobese ≥ μaverage μobese ≤ μaverage
- If the former of these is rejected, then the conclusion is that the population mean for obese patients is lower than that for average-weight patients
- If the latter is rejected, then the conclusion is that the population mean for obese patients is higher than that for average-weight patients
Questions
Interpreting non-significant results
Questions
- What does it mean to accept the null hypothesis?
- Why the null hypothesis should not be accepted?
- How a non-significant result can increase confidence that the null hypothesis is false?
- What are the problems of affirming a negative conclusion?
- When P-value is high, it means that the data provide little or no evidence that the null hypothesis is false
- The high p-value is not evidence that the null hypothesis is true
- The problem is that it is impossible to distinguish a null effect from a very small effect
- For example, in the James Bond Case Study, suppose Mr. Bond is, in fact, just barely better than chance at judging whether a Martini was shaken or stirred
- Assume he has a 0.51 probability of being correct on a given trial (π = 0.51)
- Let's say Experimenter Jones (who did not know π = 0.51) tested Mr. Bond and found he was correct 49 times out of 100 tries. * How would the significance test come out? The experimenter’s significance test would be based on the assumption that Mr. Bond has a 0.50 probability of being correct on each trial (π = 0.50). Given this assumption, the probability of his being correct 49 or more times out of 100 is 0.62
- 0.62 is far higher than 0.05
- This result, therefore, does not give even a hint that the null hypothesis is false
- However, we know (but Experimenter Jones does not) that π = 0.51 and not 0.50 and therefore that the null hypothesis is false
- So, if Experimenter Jones had concluded that the null hypothesis were true based on the statistical analysis, he or she would have been mistaken
Concluding that the null hypothesis is true is called accepting the null hypothesis. To do so is a serious error.
Questions
Steps in Hypothesis Testing
Questions
- What is the difference between a significance level and a probability level?
- What are the four steps involved in significance testing?
Step 1: State the Null Hypothesis
For a two tailed test, the null hypothesis is typically that a parameter equals zero although there are exceptions
- A typical null hypothesis is μ1 - μ2 = 0 which is equivalent to μ1 = μ2
For a one-tailed test, the null hypothesis is either that a parameter is:
- greater than or equal to zero
- less than
- equal to zero
If the prediction is that μ1 > μ2, then the null hypothesis (the reverse of the prediction) is μ1 ≤ μ2
Step 2: Specify the α level (significance level)
- Typical values are 0.05 and 0.01
Step 3: Compute the P-value
- This is the probability of obtaining a sample statistic as different or more different from the parameter specified in the null hypothesis given that the null hypothesis is true
Step 4: Compare the probability value with the α level
- If the probability value is lower then you reject the null hypothesis
- Keep in mind that rejecting the null hypothesis is not an all-or-none decision
- The lower the probability value, the more confidence you can have that the null hypothesis is false
- However, if your probability value is higher than the conventional α level of 0.05, most scientists will consider your findings inconclusive
- Failure to reject the null hypothesis does not constitute support for the null hypothesis
- It just means you do not have sufficiently strong data to reject it
Questions
Significance Testing and Confidence Intervals
Questions
- How to determine from a confidence interval whether a test is significant?
- Why a confidence interval makes clear that one should not accept the null hypothesis?
- There is a close relationship between confidence intervals and significance tests
- Specifically, if a statistic is significantly different from 0 at the 0.05 level then the 95% confidence interval will not contain 0
- All values in the confidence interval are plausible values for the parameter whereas values outside the interval are rejected as plausible values for the parameter
- In the Physicians' Reactions case study, the 95% confidence interval for the difference between means extends from 2.00 to 11.26. Therefore, any value lower than 2.00 or higher than 11.26 is rejected as a plausible value for the population difference between means
- Since zero is lower than 2.00, it is rejected as a plausible value and a test of the null hypothesis that there is no difference between means is significant
- It turns out that the p value is 0.0057. There is a similar relationship between the 99% confidence interval and Significance at the 0.01 level
- Whenever an effect is significant, all values in the confidence interval will be on the same side of zero (either all positive or all negative). Therefore, a significant finding allows the researcher to specify the direction of the effect
- There are many situations in which it is very unlikely two conditions will have exactly the same population means
- For example, it is practically impossible that aspirin and acetaminophen provide exactly the same degree of pain relief.
- Therefore, even before an experiment comparing their effectiveness is conducted, the researcher knows that the null hypothesis of exactly no difference is false
- However, the researcher does not know which drug offers more relief
- If a test of the difference is significant, then the direction of the difference is established because the values in the confidence interval are either all positive or all negative.
- If the 95% confidence interval contains zero (more precisely, the parameter value specified in the null hypothesis), then the effect will not be significant at the 0.05 level
- Looking at non-significant effects in terms of confidence intervals makes clear why the null hypothesis should not be accepted when it is not rejected: Every value in the confidence interval is a plausible value of the parameter
- Since zero is in the interval, it cannot be rejected
- However, there is an infinite number of values in the interval (assuming continuous measurement), and none of them can be rejected either.
Questions
Misconceptions
Questions
- Why the probability value is not the probability the null hypothesis is false?
- Why a low probability value does not necessarily mean there is a large effect?
- Why a non-significant outcome does not mean the null hypothesis is probably true?
Misconception 1: The probability value is the probability that the null hypothesis is false
- The probability value is the probability of a result as extreme or more extreme given that the null hypothesis is true
- It is the probability of the data given the null hypothesis
- It is NOT the probability that the null hypothesis is false.
Misconception 2: A low probability value indicates a large effect
- A low probability value indicates that the sample outcome (or one more extreme) would be very unlikely if the null hypothesis were true. A low probability value can occur with small effect sizes, particularly if the sample size is large.
Misconception 3: A non-significant outcome means that the null hypothesis is probably true
- A non-significant outcome means that the data do not conclusively demonstrate that the null hypothesis is false
Questions