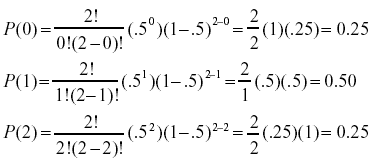Binomial Distribution
When you flip a coin, there are two possible outcomes: heads and tails.
- Each outcome has a fixed probability, the same from trial to trial.
- In the case of coins, heads and tails each have the same probability of 1/2.
More generally, there are situations in which the coin is biased, so that heads and tails have different probabilities.
- In the present section, we consider probability distributions for which there are just two possible outcomes with fixed probabilities summing to one.
- These distributions are called binomial distributions.
Example
| Outcome | First Flip | Second Flip |
|---|---|---|
| 1 | Heads | Heads |
| 2 | Heads | Tails |
| 3 | Tails | Heads |
| 4 | Tails | Tails |
The four possible outcomes that could occur if you flipped a coin twice are listed above in the table.
- Note that the four outcomes are equally likely: each has probability 1/4.
- To see this, note that the tosses of the coin are independent (neither affects the other).
- Hence, the probability of a head on Flip 1 and a head on Flip 2 is the product of P(H) and P(H), which is 1/2 x 1/2 = 1/4.
- The same calculation applies to the probability of a head on Flip 1 and a tail on Flip 2.
- Each is 1/2 x 1/2 = 1/4.
The four possible outcomes can be classified in terms of the number of heads that come up.
- The number could be two (Outcome 1), one (Outcomes 2 and 3) or 0 (Outcome 4).
- Since two of the outcomes represent the case in which just one head appears in the two tosses, the probability of this event is equal to 1/4 + 1/4 = 1/2.
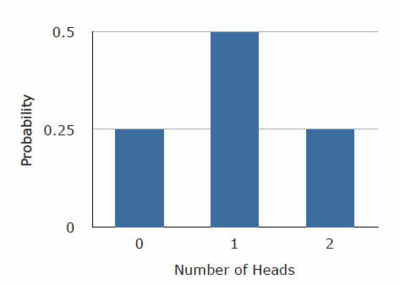
- The probabilities of these possibilities are shown in the table and figure below.
| Number of Heads | Probability |
|---|---|
| 0 | 1/4 |
| 1 | 1/2 |
| 2 | 1/4 |
The figure above is a discrete probability distribution
- It shows the probability for each of the values on the X-axis.
- Defining a head as a "success," the figure shows the probability of 0, 1, and 2 successes for two trials (flips) for an event that has a probability of 0.5 of being a success on each trial.
- This makes it an example of a binomial distribution.
The Formula for Binomial Probabilities
The binomial distribution consists of the probabilities of each of the possible numbers of successes on N trials for independent events that each have a probability of π (the Greek letter pi) of occurring.
- For the coin flip example, N = 2 and π = 0.5.
The formula for the binomial distribution is shown below:
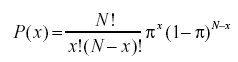 where P(x) is the probability of x successes out of N trials,
N is the number of trials, and
π is the probability of success on a given trial.
where P(x) is the probability of x successes out of N trials,
N is the number of trials, and
π is the probability of success on a given trial.
Applying this to the coin flip example,
In a spreadsheet =BINOMDIST(0,2,0.5,false)
Example
If you flip a coin twice, what is the probability of getting one or more heads?
- Since the probability of getting exactly one head is 0.50 and
- the probability of getting exactly two heads is 0.25,
- the probability of getting one or more heads is 0.50 + 0.25 = 0.75.
Now suppose that the coin is biased.
- The probability of heads is only 0.4.
* What is the probability of getting heads at least once in two tosses?
- Substituting into the general formula above, you should obtain the answer .64.
Cumulative Probabilities
We toss a coin 12 times. What is the probability that we get from 0 to 3 heads?
- The answer is found by computing the probability of exactly 0 heads, exactly 1 head, exactly 2 heads, and exactly 3 heads.
- The probability of getting from 0 to 3 heads is then the sum of these probabilities.
- The probabilities are: 0.0002, 0.0029, 0.0161, and 0.0537.
- The sum of the probabilities is 0.073.
- The calculation of cumulative binomial probabilities can be quite tedious.
- Therefore we have provided a binomial calculator to make it easy to calculate these probabilities.
Mean and Standard Deviation of Binomial Distributions
Consider a coin-tossing experiment in which you tossed a coin 12 times and recorded the number of heads. If you performed this experiment over and over again, what would the mean number of heads be?
- On average, you would expect half the coin tosses to come up heads.
- Therefore the mean number of heads would be 6.
In general, the mean of a binomial distribution with parameters N (the number of trials) and π (the probability of success on each trial) is:
μ = Nπ where μ is the mean of the binomial distribution
The variance of the binomial distribution is:
σ2 = Nπ(1-π) where σ2 is the variance of the binomial distribution
Let's return to the coin-tossing experiment.
- The coin was tossed 12 times, so N = 12.
- A coin has a probability of 0.5 of coming up heads.
- Therefore, π = 0.5.
The mean and variance can therefore be computed as follows:
μ = Nπ = (12)(0.5) = 6
σ2 = Nπ(1-π) = (12)(0.5)(1.0 - 0.5) = 3.0.
Naturally, the standard deviation (σ) is the square root of the variance (σ2).
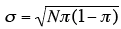
Quiz