Simulation Optimization
Jump to navigation
Jump to search
Overview
- BPMS offers simulation capabilities
- Simulation is "a means to evaluate the impact of process changes and new processes in a model environment through the creation of “what-if” scenarios"
- decisions can be tested before going life
- simulation allow forecast with a level of uncertainty
Need for Simulation Optimization
- analyst wants to find a set of model optimal performance (parameters and structure)
- range of parameter values and the number of parameter combinations is too large for analysts to simulate all possible scenarios
- they need a way to find a good solutions
Mathematical methods vs Simulation
- many problems are too complex to be modelled in analytical way
- pure optimization models alone are incapable of capturing all the complexities and dynamics of the system
- simulation cannot easily find the best solutions
- Simulation Optimization combines both methods (analytical optimization of the simulation or vice versa)
Heuristic
- Greek: "Εὑρίσκω": find, discover
- technique designed for solving a problem more quickly when classic methods are too slow
- finding an approximate solution when classic methods fail to find any exact solution (by trading optimality, completeness, accuracy, and/or precision for speed)
- e.g. rule of thumb, an educated guess, an intuitive judgement
Metaheuristic
- designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality
- make few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions
- do not guarantee an optimal solution is ever found
- implement some form of stochastic optimization.
(Wikipedia)
Metaheuristics
Problems with Simulations
- Optimization models were thought to over-simplify the real problem
- this was improved by research in metaheuristics along with improved statistical methods of analysis
Metaheuristics
- Coined in 1986 by Dr. Fred Glover
- "describe a master strategy that guides and modifies other heuristics to produce solutions beyond those that are normally generated in a quest for local optimality"
- There are algorithms to guide a series of simulations towards good results in the absence of tractable mathematical structures
- Quality of different solutions can compared
- commercial products use discrete-event or Monte Carlo simulation to performs search for optimal values of input parameters
- tool for commercial simulation software, employs metaheuristics (scatter search, tabu search, neural networks)
Optimization of Simulation Models
- develop simulation model for a system or a process
- set performance measure (for possible set of choices)
- find a configuration that produce good results
- Extreme Methods
- trial-and-error
- enumeration of all possible configurations
Applications
- configuration of machines for production scheduling
- layouts, links, and capacities for network design
- investment portfolio for financial planning
- utilization of employees for workforce planning
- course scheduling
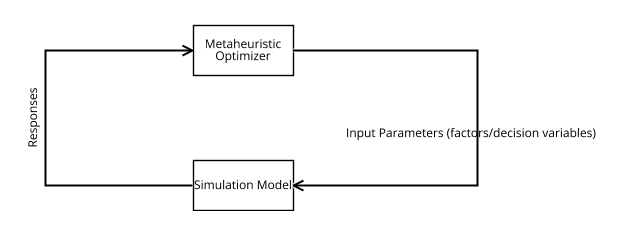
Black-box Model
- Input
- input parameters and/or structural design that lead to optimal performance (factors/levels, decision variables)
- Output
- performance measures (responses - used to model an objective function and constraints)
- Goal
- find out which factors have the greatest effect on a response
- combination of factor levels that minimizes or maximizes a response
- subject to constraints imposed on factors and/or responses
- Constraints
- constraint for both: decision variables and responses need to be formulated
- Example
- manufacturing facility
- factors - number of machines of each type, machine settings, layout, and the number of workers
- responses - cycle time, work-in-progress, and resource utilization
- goal - reduce cost, minimize cycle time, minimize resource utilization (subject to constraints)
Simulating Result
- "Changes proposed to business processes can be simulated"
- "Sensitivity of making the changes on the ultimate objectives can be examined and quantified, reducing the risk of actual implementation"
- Changes
- adding, deleting, and modifying processes
- process times
- resources required
- schedules
- skill levels
- budgets
- Performance objectives
- throughput
- costs
- inventories
- resources/capital utilization
- cash flow
- waste
Uncertaintiy
In BPM:
- simulation: a way to understand and communicate the uncertainty related to making the changes,
- optimization: provides the way to manage that uncertainty
Academic Approaches
- Stochastic approximation (gradient-based approaches)
- (sequential) response surface methodology
- random search
- sample path optimization (also known as stochastic counterpart)
Pragmatic Approach
- Commercial simulation software employs metaheuristics
Evolutionary Approaches
- commercial simulation uses evolutionary approaches
- Evolutionary approaches: builds and evolves population of solutions
- e.g. Genetic Algorithms and Scatter Search.
- a simulation model can be thought of as a
“mechanism that turns input parameters into output performance measures” (Law and Kelton, 1991)
- simulation model is a function that evaluates the merit of a set of specifications, typically represented as set of values
- Looking at simulation model as a function encouraged family of approaches to optimize simulations based on response surfaces and metamodels.
Constraints
- speciying constraints is important feature of simulation optimization
- constraints define the feasibility of trial solutions
- specified as mathematical expressions or as logic statements
- usually formulated with input factors or/and responses
Constraints and Feasability
- constraints in a simulation optimization model depend only on input parameters -> new trial solution can be checked for feasibility before running the simulation
- infeasible trial solution may be discarded or may be mapped to a feasible one when its feasibility depends only on constraints formulated with input parameters
- constraints depend on responses -> feasibility of a solution is not known before running the simulation

