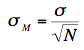Power of a test
Introduction to Power
Define power
- Suppose you work for a foundation whose mission is to support researchers in mathematics education and your role is to evaluate grant proposals and decide which ones to fund.
- You receive a proposal to evaluate a new method of teaching high-school algebra.
- The research plan is to compare the achievement of students taught by the new method with those taught by the traditional method.
- The proposal contains good theoretical arguments why the new method should be superior and the proposed methodology is sound.
- In addition to these positive elements, there is one important question still to be answered: Does the experiment have a high probability of providing strong evidence that the new method is better than the standard method even if, in fact, the new method is actually better?
- It is possible, for example, that the proposed sample size is so small that even a fairly large population difference would be difficult to detect.
- That is, if the sample size is small, then even a fairly large difference in sample means might not be significant.
- If the difference is not significant, then no strong conclusions can be drawn about the population means.
- It is not justified to conclude that the null hypothesis that the population means are equal is true just because the difference is not significant.
- Of course, it is not justified to conclude that this null hypothesis is false. Therefore, when an effect is not significant, the result is inconclusive.
- You may prefer that your foundation's money be used to fund a project that has a higher probability of being able to make a strong conclusion.
- Power is defined as the probability of correctly rejecting a false null hypothesis.
- In terms of our example, it is the probability that given there is a difference between the population means of the new method and the standard method, the sample means will be significantly different.
- The probability of failing to reject a false null hypothesis is often referred to as β.
- Therefore power can be defined as:
:
power = 1 - β.
Identify situations in which it is important to estimate power
- It is very important to consider power while designing an experiment.
- You should avoid spending a lot of time and/or money on an experiment that has little chance of finding a significant effect.
Questions
Template:Statistics Links
Power | Example Calculations >
Example Calculations
Compute power using the binomial distribution
In the "Shaking and Stirring Martinis" case study, the question was whether Mr. Bond could tell the difference between martinis that were stirred and martinis that were shaken. For the sake of this example, assume he can tell the difference and is able to correctly state whether a martini had been shaken or stirred 0.75 of the time. Now, suppose an experiment is being conducted to investigate whether Mr. Bond can tell the difference. Specifically is Mr. Bond correct more than 0.50 of the time. We know that he can (that's an assumption of the example). However, the experimenter does not know and asks Mr. Bond to judge 16 Martinis. The experimenter will do a significance test based on the binomial distribution. Specifically, if a one tailed test is significant at the 0.05 level then he or she will conclude that Mr. Bond can tell the difference. The probability value is computed assuming the null hypothesis is true (π = 0.50). Therefore, the experimenter will determine how many times Mr. Bond is correct, and compute the probability of being correct that many or more times given that the null hypothesis is true. The question is: what is the probability the experimenter will correctly reject the null hypothesis that π = 0.50? In other words, what is the power of this experiment.
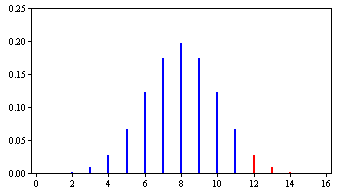
The binomial distribution for N = 16 and π = 0.50 is shown in Figure 1. The probability of being correct on 11 or more trials is 0.105 and the probability of being correct on 12 or more trials is 0.038. Therefore, the probability of being correct on 12 or more trials is less than 0.05. This means that the null hypothesis will be rejected if Mr. Bond is correct on 12 or more trials and will not be rejected otherwise.
Figure 1. The binomial distribution for N = 16 and π = 0.50.
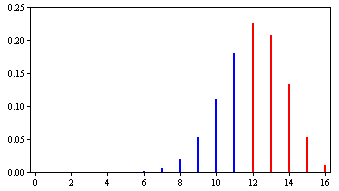
We know that Mr. Bond is correct 0.75 of the time. (Obviously the experimenter does not know this or there would be no need for an experiment.) The binomial distribution with N = 16 and π = 0.75 is shown in Figure 2.
Figure 2. The binomial distribution for N = 16 and π = 0.75.
The probability of being correct on 12 or more trials is 0.63. Therefore, the power of the experiment is 0.63.
To sum up, the probability of being correct on 12 or more trials given that the null hypothesis is true is less than 0.05. Therefore, if Mr. Bond is correct on 12 or more trials, the null hypothesis will be rejected. Given Mr. Bond's true ability to be correct on 0.75 of the trials, the probability he will be correct on 12 or more trials is 0.63. Therefore power is 0.63.
Compute power using the normal distribution
In the section on Testing a Single Mean for significance, the first example was based on the assumption that the experimenter knew the population variance. Although this is rarely true in practice, the example is very useful for pedagogical purposes. For the same reason, the following example assumes the experimenter knows the population variance. Power calculators are available for situations in which the experimenter does not know the population variance.
Suppose a math achievement test were known to have a mean of 75 and standard deviation of 10. A researcher is interested in whether a new method of teaching results in a higher mean. Assume that although the experimenter does not know it, the population mean for the new method is 80. The researcher plans to sample 25 subjects and do a one-tailed test of the whether the sample mean is significantly higher than 75. What is the probability that the researcher will correctly reject the false null hypothesis that the population mean is 75? The following shows how this probability is computed.
The researcher assumes that the population standard deviation with the new method is the same as with the old method (10) and that the distribution is normal. Since the population standard deviation is assumed to be known, the researcher can use the normal distribution rather than the t distribution to compute the p value. Recall that the standard error of the mean (σM) is
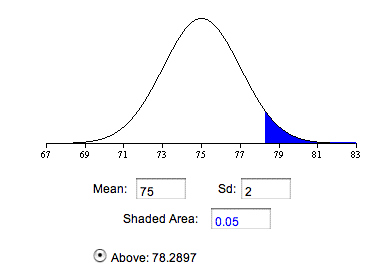
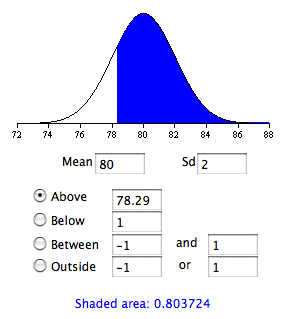
which is equal to 10/5 = 2 in this example. As can be seen in Figure 3, if the null hypothesis that the population mean equals 75 is true, then the probability of a sample mean being greater than or equal to 78.29 is 0.05. Therefore, the experimenter will reject the null hypothesis if the sample mean, M, is 78.29 or larger.
Figure 3. The sampling distribution of the mean if the null hypothesis is true. (figure created with the Inverse Normal Calculator)
The question, then, is what is the probability the experimenter gets a sample mean greater than 78.29 given that the population mean is 80? Figure 4 shows that this probability is 0.80.
Figure 4. The sampling distribution of the mean if the population mean is 75. The test is significant if the sample mean is 78.29 or higher. (figure created with the Normal Calculator)
Therefore, the probability that the experimenter will reject the null hypothesis that the null hypothesis is 75 is 0.80. In other words, power = 0.80.
Use a power calculator to compute power for the t distribution
Calculation of power is more complex for t-tests and for Analysis of Variance. The power calculator computes power for a t test of independent groups. Calculators for other types of designs can be found at this
Russ Lenth's Power Calculators (external link)
Questions
Template:Statistics Links
< Introduction to Power | Power Demo 1 >
Power Demo 1
simulations/power/power_sample_size.html
< Example Calculations | Power Demo 2 >
Template:Statistics Links
Power Demo 2
simulations/power2/power2.html
< Power Demo 1 | Factors Affecting Power >
Template:Statistics Links
Factors Affecting Power
Prerequisites
- Introduction to Power, Example Calculations, Significance Testing, Type I and II Errors, One- and Two-Tailed Tests
This chapter state five factors affecting power and what the effect of each of them is
Several factors affect the power of a statistical test. Some of the factors are under the control of the experimenter whereas others are not. The following example will be used to illustrate the various factors.
Suppose a math achievement test were known to be normally distributed with a mean of 75 and standard deviation of σ. A researcher is interested in whether a new method of teaching results in a higher mean. Assume that although the experimenter does not know it, the population mean μ is larger than 75. The researcher plans to sample N subjects and do a one-tailed test of the whether the sample mean is significantly higher than 75. In this section we consider factors that affect the probability that the researcher will correctly reject the false null hypothesis that the population mean is 75? In other words, factors that affect power.
Sample Size
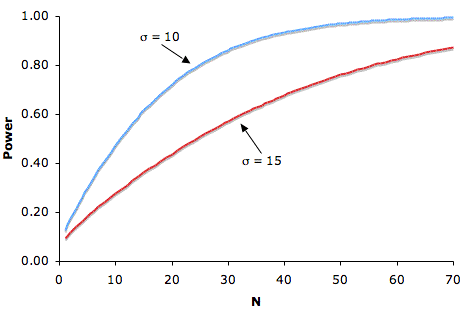
Figure 1 shows that the larger the sample size, the higher the power. Since sample size is typically under an experimenter's control, increasing sample size is one way to increase power. However, it is sometimes difficult and/or expensive to use a large sample size.
Figure 1. The relationship between sample size and power for H0: μ = 75, real μ = 80, one-tailed α = 0.05, for σ's of 10 and 15.
Standard Deviation
Figure 1 also shows that power is higher when the standard deviation is small than when it is large. For all values of N, power is higher for the standard deviation of 10 than for the standard deviation of 15 (except, of course, when N = 0). Experimenters can sometimes control the standard deviation by sampling from a homogeneous population of subjects, by reducing random measurement error, and/or by making sure the experimental procedures are applied very consistently.
Difference between Hypothesized and True Mean
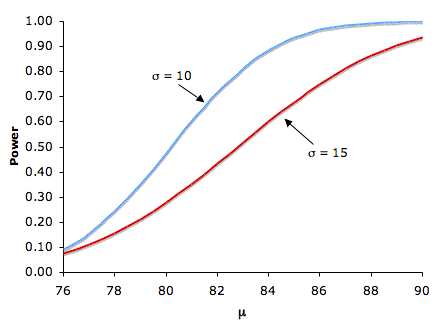
Naturally, the larger the effect size, the more likely it is that an experiment would find a significant effect. Figure 2 shows the effect of increasing the difference between the mean specified by the null hypothesis (75) and the population mean μ for standard deviations of 10 and 15.
Figure 2. The relationship between power and μ with H0: μ = 75, one-tailed α = 0.05, for σ's of 10 and 15.
Significance Level
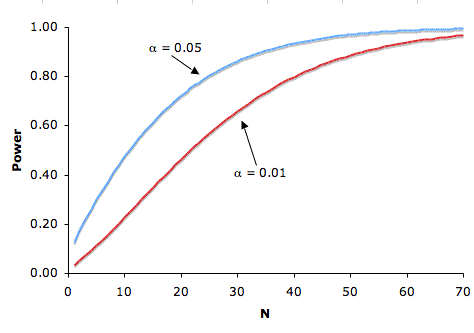
There is a tradeoff between the significance level and power: the more stringent (lower) the significance level, the lower the power. Figure 3 shows that power is lower for the 0.01 level than it is for the 0.05 level. Naturally, the stronger the evidence needed to reject the null hypothesis, the lower the chance that the null hypothesis will be rejected.
Figure 3. The relationship between power and significance level with one-tailed tests: μ = 75, real μ = 80, and σ = 10.
One- versus Two-Tailed Tests
Power is higher with a one-tailed test than with a two-tailed test as long as the hypothesized direction is correct. A one-tailed test at the 0.05 level has the same power as a two-tailed test at the 0.10 level. A one-tailed test, in effect, raises the significance level.
Questions
Power | Example Calculations >
Template:Statistics Links < Power Demo 2 | Power Exercises >
Exercises
1. Exercise
Define power in your own words.
2. Exercise
List 3 measures one can take to increase the power of an experiment. Explain why your measures result in greater power.
3. Exercise
Population 1 mean = 36
Population 2 mean = 45
Both population variances are 10.
What is the probability that a t test will find a significant difference between means at the 0.05 level? Give results for both one- and two-tailed tests.
Hint: the power of a one-tailed test at 0.05 level is the power of a two-tailed test at 0.10.
4. Exercise
Rank order the following in terms of power.
| Population 1 Mean | n | Population 2 Mean | Variance | |
|---|---|---|---|---|
| a | 29 | 20 | 43 | 12 |
| b | 34 | 150 | 40 | 6 |
| c | 105 | 24 | 50 | 27 |
| d | 314 | 4 | 120 | 10 |
| e | 30 | 31 | 41 | 8 |
5. Exercise
Alan, while snooping around his grandmother's basement stumbled upon a shiny object protruding from under a stack of boxes . When he reached for the object a genie miraculously materialized and stated: "You have found my magic coin. If you flip this coin an infinite number of times you will notice that heads will show 60% of the time." Soon after the genie's declaration he vanished, never to be seen again. Alan, excited about his new magical discovery, approached his friend Ken and told him about what he had found. Ken was skeptical of his friend's story, however, he told Alan to flip the coin 100 times and to record how many flips resulted with heads.
(a) What is Ken's null hypothesis?
(b) What is the probability that Alan will be able convince Ken that his coin has special powers by finding a p value below 0.05 (one tailed). Use the Binomial Calculator (and some trial and error)
(c) If Ken told Alan to flip the coin only 20 times, what is the probability that Alan will not be able to convince Ken (by failing to reject the null hypothesis at the 0.05 level)?