One- and Two-Tailed Tests

Prerequisites

• Binomial Distribution, Introduction to Hypothesis Testing, Statistical Significance

Questions

• When to use one-tailed and when two-tailed test?

One-tailed probability

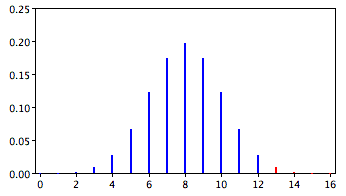
• In the James Bond case study, Mr. Bond was given 16 trials on which he judged whether a martini had been shaken or stirred
• He was correct on 13 of the trials
• From the binomial distribution, we know that the probability of being correct 13 or more times out of 16 if one is only guessing is 0.0106

• The red bars show the values greater than or equal to 13
• As you can see in the figure, the probabilities are calculated for the upper tail of the distribution
• A probability calculated in only one tail of the distribution is called a one-tailed probability

Two-tailed probability

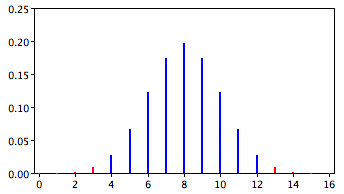
• A slightly different question can be asked of the data: "What is the probability of getting a result as extreme or more extreme than the one observed"?
• Since the chance expectation is 8/16, a result of 3/16 is equally as extreme as 13/16
• Thus, to calculate this probability, we would consider both tails of the distribution
• Since the binomial distribution is symmetric when π = 0.5, this probability is exactly double the probability of 0.0106 computed previously
• Therefore, p = 0.0212
• A probability calculated in both tails of a distribution is called a two-tailed probability

One-tailed vs Two-tailed

Should the one-tailed or the two-tailed probability be used to assess Mr. Bond's performance? That depends on the way the question is posed:

One-tailed

• Is Mr. Bond is better than chance at determining whether a Martini is shaken or stirred?

 H0: π ≤ 0.5
 H1: π ≥ 0.5
 H0 rejected only if the sample proportion is much greater than 0.50.

What would the one-tailed probability be if Mr. Bond was correct on only three of the sixteen trials?

• Since the one-tailed probability is the probability of the right-hand tail, it would be the probability of getting three or more correct out of 16.
• This is a very high probability and the null hypothesis would not be rejected.

Two-tailed

• Can Mr. Bondn tell the difference between shaken or stirred martinis?
• We would conclude he could tell the difference if:
  • he performed either much better than chance
  • or much worse than chance

• If he performed much worse than chance, we would conclude that he can tell the difference, but he does not know which is which
• Therefore, since we are going to reject the null hypothesis if Mr. Bond does either very well or very poorly, we will use a two-tailed probability

H0: π = 0.5
H1: π ≠ 0.5
H0 rejected if the sample proportion correct deviates greatly from 0.5 in either direction

How to decide?

• You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data
• Tests that compute one-tailed probabilities are called one-tailed tests; those that compute two-tailed probabilities are called two-tailed tests

One-tailed tests	Two-tailed tests
more common in scientific research because an outcome signifying that something other than chance is operating is usually worth noting	appropriate when it is not important to distinguish between no effect and an effect in the unexpected direction
Questions like: is A better than B	Questions like: is A has any effect on B

Common Cold Treatment

• For example, consider an experiment designed to test the efficacy of treatment for the common cold
• The researcher would only be interested in whether the treatment was better than a placebo control.
• It would not be worth distinguishing between the case in which the treatment was worse than a placebo and the case in which it was the same because in both cases the drug would be worthless

• Even if the researcher predicts the direction of an effect, the two-tailed test might be more appropriate
• If the effect comes out strongly in the non-predicted direction, the researcher is not justified in concluding that the effect is not zero
• Since this is unrealistic, one-tailed tests are usually viewed skeptically if justified on this basis alone.

Questions

1 Select all that apply. Which is/are true of two-tailed tests?

	They are appropriate when it is important to distinguish between no effect and an effect in any direction.
	They are more common than one-tailed tests.
	They compute two-tailed probabilities.
	They are more controversial than one-tailed tests.

Answer >>

Two-tailed tests look for an effect in either direction, so they compute two-tailed probabilities. They are much more common than one-tailed tests in scientific research because an outcome signifying that something other than chance is operating is usually worth noting. Some people disagree with the use of one-tailed tests except in very specific situations.

2 You are testing the difference between college freshmen and seniors on a math test. You think that the seniors will perform better, but you are still interested in knowing if the freshmen perform better. What is the null hypothesis?

	The mean of the seniors is less than or equal to the mean of the freshmen
	The mean of the seniors is greater than or equal to the mean of the freshmen
	The mean of the seniors is equal to the mean of the freshmen

Answer >>

Because you are interested in the effect in either direction, you will use a two-tailed test. Thus, the null hypothesis is that the mean of the seniors is equal to the mean of the freshmen.

3 You think a coin is biased, and you are interested in finding out if it is. What is the probability that out of 30 flips, it will come up one side 8 or fewer times? Write your answer out to three decimal places.

Answer >>

This question is asking you to compute a two-tailed probability.

4 You think a coin is biased and will come up heads more often than it will come up tails. What is the probability that out of 22 flips, it will come up heads 16 or more times? Write your answer out to three decimal places.

Answer >>

This question is asking you to compute a one-tailed probability. Using the binomial calculator with the values of N is equal to 22, p is equal to 0.5, and greater than or equal to 16, you get p equal to 0.0262.

Template:Statistics Links < Type I and II Errors | Significant Results >