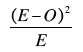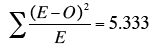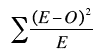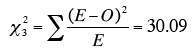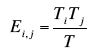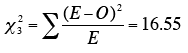Chi-square
<slideshow style="nobleprog" headingmark="。" incmark="…" scaled="false" font="Trebuchet MS" >
- title
- Chi-Square Distribution
- author
- Yolande Tra
</slideshow>
Chi-Square Distribution
Prerequisites
- Distributions, Standard Normal Distribution, Degrees of Freedom
Define the Chi Square distribution in terms of squared normal deviates
- The Chi Square Distribution is the distribution of the sum of squared standard normal deviates
- The degrees of freedom of the distribution is equal to the number of standard normal deviates being summed
- Therefore, Chi Square with one degree of freedom, written as χ2(1), is simply the distribution of a single normal deviate squared
- The area of a Chi Square distribution below 4 is the same as the area of a standard normal distribution below 2 since 4 is 22.
Example。
- You sample two scores from a standard normal distribution, square each score, and sum the squares.
- What is the probability that the sum of these two squares will be six or higher?
- Since two scores are sampled, the answer can be found using the Chi Square distribution with two degrees of freedom
- A Chi Square calculator can be used to find that the probability of a Chi Square (with 2 df) of being six or higher is 0.05
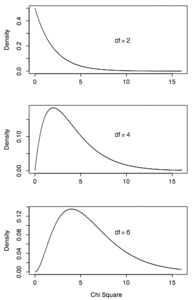
How does the shape of the Chi Square distribution change its degrees of freedom increase?
- The mean of a Chi Square distribution is its degrees of freedom.
- Chi Square distributions are positively skewed, with the degree of skew decreasing with increasing degrees of freedom
- As the degrees of freedom increase, the Chi Square Distribution approaches a normal distribution
- Notice how the skew decreases as the degrees of freedom increases.
Where can we use Chi Square distribution ?。
- The Chi Square distribution is very important because many test statistics are approximately distributed as Chi Square
- Two of the more commonly tests using the Chi Square distribution are:
- tests of deviations of differences between theoretically expected and observed frequencies (one-way tables)
- the relationship between categorical variables (contingency tables)
- Numerous other tests beyond the scope of this work are based on the Chi Square distribution.
Questions
Template:Statistics Links
Chi Square | One-Way Tables >
One-Way Tables。
Objectives
- Describe what it means for there to be theoretically-expected frequencies
- Compute expected frequencies
Expected frequencies
- The Chi Square distribution can be used to test whether observed data differ significantly from theoretically expectations
- For example, for a fair six-sided die, the probability of of any given outcome on a single roll would be 1/6
- The data in Table 1 were obtained by rolling a six-sided die 36 times
- However, as can be seen in Table 1, some outcomes occurred more frequently than others
- For example a "3" came up nine times whereas a "4" came up only two times
- Are these data consistent with the hypothesis that the die is a fair die?
。
- Naturally, we do not expect the sample frequencies of the six possible outcomes throws to be the same since chance differences will occur
- So, the finding that the frequencies differ does not mean that the die is not fair
- One way to test whether the die is fair is to conduct a significance test
- The null hypothesis is that the die is fair
- This hypothesis is tested by computing the probability of obtaining frequencies as discrepant or more discrepant from a uniform distribution of frequencies as obtained in the sample
- If this probability is sufficiently low, then the null hypothesis that the die is fair can be rejected.
。
Table 1. Outcome Frequencies from a Six-Sided Die.
| Outcome | Frequency |
|---|---|
| 1 | 8 |
| 2 | 5 |
| 3 | 9 |
| 4 | 2 |
| 5 | 7 |
| 6 | 5 |
。
The first step in conducting the significance test is to compute the expected frequency for each outcome given that the null hypothesis is true. For example, the expected frequency of a "1" is 6 since the probability of a "1" coming up is 1/6 and there were a total of 36 rolls of the die.
Expected frequency = (1/6)(36) = 6
Note that the expected frequencies are expected only in a theoretical sense. We do not really "expect" the observed frequencies to match the "expected frequencies" exactly.
The calculation continues as follows. Letting E be the expected frequency of an outcome and O be the observed frequency of that outcome, compute
for each outcome. Table 2 shows these calculations.
。
Table 2. Outcome Frequencies from a Six-Sided Die.
| Outcome | E | O | |
|---|---|---|---|
| 1 | 6 | 8 | 0.667 |
| 2 | 6 | 5 | 0.167 |
| 3 | 6 | 9 | 1.500 |
| 4 | 6 | 2 | 2.667 |
| 5 | 6 | 7 | 0.167 |
| 6 | 6 | 5 | 0.167 |
。
Next we add up all the values in Column 4 of Table 2.
This sampling distribution of
is approximately distributed as Chi Square on k-1 degrees of freedom where k is the number of categories. Therefore, for this problem the test statistic is
χ25
which means the value of Chi Square with 5 degrees of freedom is 5.333.
From a Chi Square calculator it can be determined that the probability of a Chi Square of 5.333 or larger is 0.377. Therefore, the null hypothesis that the die is fair cannot be rejected.
Compute Chi Square。
This Chi Square test can also be used to test other deviations between expected and observed frequencies. The following example shows a test of whether the variable "University GPA" in the SAT and College GPA case study is normally distributed.
The second column of Table 3 shows the proportions of a normal distribution falling between various limits. The expected frequencies (E) are calculated by multiplying the number of scores (105) by the proportion. The final column shows the observed number of scores in each range. It is clear that the observed frequencies vary greatly from the expected frequencies. Note that if the distribution were normal then there would have been only about 35 scores between 0 and 1 whereas 60 were observed.
。
Table 3. Expected and Observed Scores for 105 University GPA Scores.
| Range | Proportion | E | O |
|---|---|---|---|
| Above 1 | 0.159 | 16.695 | 9 |
| 0 to 1 | 0.341 | 35.805 | 60 |
| -1 to 0 | 0.341 | 35.805 | 17 |
| Below -1 | 0.159 | 16.695 | 19 |
Determine the degrees of freedom。
The test of whether the observed scores deviate significantly from the expected is computed using the familiar calculation.
The subscript "3" means there are three degrees of freedom. As before, the degrees of freedom is the number of outcomes minus 1, which is 4-1=3 in this example. The Chi Square distribution calculator shows that p < 0.001 for this Chi Square. Therefore, the null hypothesis that the scores are normally distributed can be rejected.
Questions
Template:Statistics Links < Chi Square Distribution | Testing Distributions Demo >
Testing Distribution Demo
simulations/chi_theor/chi_theor.html
Template:Statistics Links < One-Way Tables | Contingency Tables >
Contingency Tables
Prerequisites
Null hypothesis. Expected cell frequencies。
This section shows how to use Chi Square to test the relationship between nominal variables for significance. For example, Table 1 shows the data from the Mediterranean Diet and Health case study.
Table 1. Frequencies for Diet and Health Study (Outcome).
| Diet | Cancers | Fatal Heart Disease | Non-Fatal Heart Disease | Healthy | Total |
|---|---|---|---|---|---|
| AHA | 15 | 24 | 25 | 239 | 303 |
| Mediterranean | 7 | 14 | 8 | 273 | 302 |
| Total | 22 | 38 | 33 | 512 | 605 |
。
The question is whether there is a significant relationship between diet and outcome. The first step is to compute the expected frequency for each cell based on the assumption that there is no relationship. These expected frequencies are computed from the totals as follows. We begin by computing the expected frequency for the AHA Diet/Cancers combination. Note that 22/605 subjects developed cancer. The proportion who developed cancer is therefore 0.0364. If there were no relationship between diet and outcome, then we would expect 0.0364 of those on the AHA diet to develop cancer. Since 303 subjects were on the AHA diet, we would expect (0.0364)(303) = 11.02 cancers on the AHA diet. Similarly, we would expect (0.0364)(302) = 10.98 cancers on the Mediterranean diet. In general, the expected frequency for a cell in the ith row and the jth column is equal to
where Ei,j is the expected frequency for cell i,j, Ti is the total ith row, Tj is the total for the jth column, and T is the total number of observations. For the AHA Diet/Cancers cell, i = 1, j = 1, Ti = 303, Tj = 22, and T = 605. Table 2 shows the expected frequencies (in parenthesis) for each cell in the experiment.
。
Table 2. Observed and Expected Frequencies for Diet and Health Study (Outcome).
| Diet | Cancers | Fatal Heart Disease | Non-Fatal Heart Disease | Healthy | Total |
|---|---|---|---|---|---|
| AHA | 15 (11.02) | 24 (19.03) | 25 (16.53) | 239 (256.42) | 303 |
| Mediterranean | 7 (10.98) | 14 (18.97) | 8 (16.47) | 273 (255.58) | 302 |
| Total | 22 | 38 | 33 | 512 | 605 |
。
The significance test is conducted by computing Chi Square as follows.
The degrees of freedom is equal to (r-1)(c-1) where r is the number of rows and c is the number of columns. For this example, the degrees of freedom is (2-1)(4-1) = 3. The Chi Square calculator can be used to determine that the probability value for a Chi Square of 16.55 with three degrees of freedom is less 0.0009. Therefore, the null hypothesis of no relationship between diet and outcome can be rejected.
Compute Chi Square and df。
A key assumption of the Chi Square test of independence is that each subject contributes data to only one cell. Therefore the sum of all cell frequencies in the table must be the same as the number of subjects in the experiment. Consider an experiment in which each of 16 subjects each attempted two anagram problems. The data are shown in Table 3.
Table 3. Anagram Problem Data.
| Anagram 1 | Anagram 2 | |
|---|---|---|
| Solved | 10 | 4 |
| Did not Solve | 6 | 12 |
It would not be valid to use the Chi Square test on these data since each subject contributed data to two cells: one cell based on their performance on Anagram 1 and one cell based on their performance on Anagram 2. The total of the cell frequencies in the table is 32 but the total number of subjects is only 16.
The formula for Chi Square yields a statistic that is only approximately a Chi Square distribution. In order for the approximation to be adequate, the total number of subjects should be at least 20. Some authors claim that the correction for continuity should be used whenever an expected cell frequency is below 5. Research in statistics has shown that this practice is not advisable. For example, see:
Bradley, D. R., Bradley, T. D., McGrath, S. G., & Cutcomb, S. D. (1979) Type I error rate of the chi square test of independence in r x c tables that have small expected frequencies. Psychological Bulletin, 86, 1200-1297.
The correction for continuity when applied to 2 x 2 contingency tables is called the Yates correction. The simulation 2 x 2 tables lets you explore the accuracy of the approximation and the value of this correction.
Questions
Template:Statistics Links < Testing Distributions Demo | 2 x 2 Table Simulation >
2 x 2 Table Simulation。
simulations/contingency/contingency.html
Template:Statistics Links < Contingency Tables | Chi Square Exercises >
Exercises。
1. Exercise
A die is suspected of being biased. It is rolled 25 times with the following result:
| Outcome | Frequency |
|---|---|
| 1 | 9 |
| 2 | 4 |
| 3 | 1 |
| 4 | 8 |
| 5 | 3 |
| 6 | 0 |
Conduct a significance test to see if the die is biased. What Chi Square value do you get and how many degrees of freedom does it have? (relevant section)
。
2. Exercise
A recent experiment investigated the relationship between smoking and urinary incontinence. Of the 322 subjects in the study who were incontinent, 113 were smokers, 51 were former smokers, and 158 had never smoked. Of the 284 control subjects who were not incontinent, 68 were smokers, 23 were former smokers, and 193 had never smoked. (a) Create a table displaying this data. b) What is the expected frequency in each cell? (relevant section)
。
3. Exercise
At a school pep rally, a group of sophomore students organized a free raffle for prizes. They claim that they put the names of all of the students in the school in the basket and that they randomly drew 36 names out of this basket. Of the prize winners, 6 were freshmen, 14 were sophomores, 9 were juniors, and 7 were seniors. The results do not seem that random to you. You think it is a little fishy that sophomores organized the raffle and also won the most prizes. Your school is composed of 30% freshmen, 25% sophomores, 25% juniors, and 20% seniors. Conduct a significance test to determine whether the winners of the prizes were distributed throughout the classes as would be expected based on the percentage of students in each group. Report your Chi Square and p values. (relevant section)
。
4. Exercise
Some parents of the West Bay little leaguers think that they are noticing a pattern. There seems to be a relationship between the number on the kids' jerseys and their position. These parents decide to record what they see. The hypothetical data appear below. Conduct a Chi Square test to determine if the parents' suspicion that there is a relationship between jersey number and position is right. Report your Chi Square and p values. (relevant section)
| Infield | Outfield | Pitcher | Total | |
|---|---|---|---|---|
| 0-9 | 12 | 5 | 5 | 22 |
| 10-19 | 5 | 10 | 2 | 17 |
| 20+ | 4 | 4 | 7 | 15 |
| Total | 21 | 19 | 14 | 54 |
。
Answers:
1) (a) Chi Square = 16.0, df = 5
2) (b) Incontinent/Smoker cell: 96.2
3) (b) p = .18
4) Chi Square = 10.2