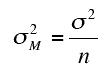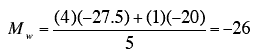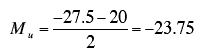Introduction

Questions

What null hypothesis is tested by ANOVA?
What are the uses of ANOVA?

What is ANOVA?

Analysis of Variance (ANOVA) is a statistical method used to compare two or more means
Inferences about means are made by analyzing variance (therefore it is not called analysis of mean)
ANOVA is used to test general rather than specific differences among means

Smiles and Leniency Example

Let us investigate types of smiles on the leniency
Types of smiles: neutral, false, felt, miserable

The results from the Tukey hsd test (Six Pairwise Comparisons):

Comparison	Mi-Mj	Q	p
False - Felt	0.46	1.65	0.649
False - Miserable	0.46	1.65	0.649
False - Neutral	1.25	4.48	0.010
Felt - Miserable	0.00	0.00	1.000
Felt - Neutral	0.79	2.83	0.193
Miserable - Neutral	0.79	2.83	0.193

Notice that the only significant difference is between the False and Neutral conditions.
ANOVA tests the non-specific null hypothesis that all four populations means are equal

μ_false = μ_felt = μ_miserable = μ_neutral

This non-specific null hypothesis is sometimes called the omnibus null hypothesis
When the omnibus null hypothesis is rejected, the conclusion is that at least one population mean is different from at least one other mean
ANOVA does not reveal which means are different from which
It offers less specific information than the Tukey hsd test
The Tukey hsd is therefore preferable to ANOVA in this situation

Why to use ANOVA instead of HSD Tukey

There are complex types of analyses that can be done with ANOVA and not with the Tukey test
ANOVA is by far the most commonly-used technique for comparing means
Is important to understand ANOVA in order to understand research reports.

Questions

	True
	False

Answer >>

False, the omnibus null is that all group means are the same.

	True
	False

Answer >>

True, An analysis of variance (ANOVA) is most often used to determine if there are differences among 3 or more group means. However, if there are more than 2 groups an ANOVA does not provide information regarding where the differences lie.

	True
	False

Answer >>

False, both t-tests and ANOVAs use both. In a t test the difference between means is in the numerator. In an ANOVA, the variance of the grouop means (multiplied by n) is in the numerator.

	True
	False

Answer >>

True, the Tukey HSD controls the Type I error rate and is valid without first running an ANOVA.

Template:Statistics Links

ANOVA designs

Questions

What are factors and levels of each factor?
What is a between-subjects or a within-subjects factor
What is factorial design
What kind of types of experimental designs can be analyzed by ANOVA?

Factors and Levels

In the case study Smiles and Leniency, the effect of different types of smiles on the leniency showed to a person was investigated
Type of smile (neutral, false, felt, miserable) is independent variable or factor
"Type of Smile" has four levels

Single or Multi factor ANOVA

An ANOVA conducted on a design in which there is only one factor is called a one-way ANOVA
If an experiment has two factors, then the ANOVA is called a two-way ANOVA

Suppose an experiment on the effects of age and gender on reading speed were conducted using three age groups (10 yr, 15 yr, and 20 yr) and the two genders (males and females)

What are the factors and levels in this experiment?

Answer >>

The factors would be age and gender. Age would have three levels and gender would have two levels

Between- and Within-Subject Factors

Between-subjects

In the Smiles and Leniency study, the four levels of the factor "Type of Smile" were represented by four separate groups of subjects
When different subjects are used for the levels of the factor, the factor is called a between-subjects factor or a between-subjects variable
The term "between subjects" reflects the fact that comparisons are between different groups of subjects.

Within-subjects

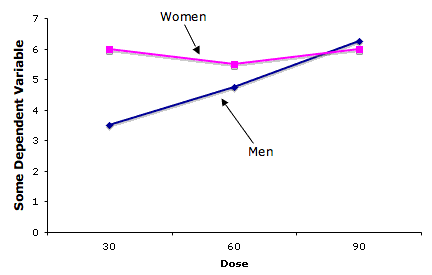
In the ADHD Treatment Study, every subject was tested with each of four dosage levels (0, 0.15, 0.30, 0.60 mg/kg) of a drug
Therefore there was only one group of subjects and comparisons were not between different groups of subjects but between conditions within the same subjects
When the same subjects are used for the levels of the factor, the factor is called a within-subjects factor or within-subjects variable
Within-subjects variables are sometimes referred to as repeated-measures variables since there are repeated measurements of the same subjects.

Multi-Factor Designs

Consider a hypothetical study of the effects of age and gender on reading speed in which males and females from the age levels of 8 years, 10 years, and 12 years were tested.
There would be a total of six different groups:

Group	Gender	Age
1	Female	8
2	Female	10
3	Female	12
4	Male	8
5	Male	10
6	Male	12

This design has two factors: age and gender
- age has three levels
- gender has two levels

When all combinations of the levels are included (as they are here) the design is called a factorial design
A concise way of describing this design is as a Gender (2) x Age (3) factorial design where the numbers in parentheses indicate the number of levels
Complex designs frequently have more than two factors and may have combinations of between- and within-subject factors.

Questions

Template:Statistics Links

One-Factor ANOVA (Between-Subjects)

Questions

What does the Mean Square Error estimates when the null hypothesis is true and when the null hypothesis is false?
What does the Mean Square Between estimates when the null hypothesis is true and when the null hypothesis is false?
What are the assumptions of a one-way ANOVA
How to compute MSB
How to compute MSE
How to compute F and the two degrees of freedom parameters
Describe the shape of the F distribution
Why is ANOVA best thought of as a two-tailed test even though literally only one tail of the distribution is used
What is the relationship between the t and F distributions
How to partition the sums of squares into conditions and error

One-factor between-subjects design

In Smiles and Leniency case study there were four conditions with 34 subjects in each condition
There was one score per subject
The null hypothesis tested by ANOVA is that the population means for all conditions are the same.

H0: μ_false = μ_felt = μ_miserable = μ_neutral

If the null hypothesis is rejected, then it can be concluded that at least one of the population means is different from at least one other population means.

Analysis of variance

Analysis of variance is a method for testing differences among means by analyzing variance

The test is based on two estimates of the population variance (σ²)

Mean Square Error (MSE)

based on differences among scores within the groups
MSE estimates σ² regardless of whether the null hypothesis is true (the population means are equal)

Mean Square Between (MSB)

based on differences among the sample means
MSB only estimates σ² if the population means are equal
If the population means are not equal, then MSB estimates a quantity larger than σ²

MSB and MSE

If the MSB is much larger than the MSE, then the population means are unlikely to be equal
If the MSB is about the same as MSE, then the data are consistent with the hypothesis that the population means are equal.

ANOVA Assumptions

The populations have the same variance (homogeneity of variance)
The populations are normally distributed
Each value is sampled independently from each other value

The last assumption requires that each subject provide only one value
If a subject provides two scores, then the value are not independent
The analysis of data with two scores per subject is shown in the section on within-subjects ANOVA

These assumptions are the same as for a t test of differences between groups except that it applies to two or more groups, not just to two groups.

The means and variances of the four groups in the Smiles and Leniency case study are shown below
There are 34 subjects in each of the four conditions (False, Felt, Miserable, and Neutral).

Means and Variances from Smiles and Leniency Study.

Condition	Mean	Variance
False	5.376	3.3380
Felt	4.9118	2.8253
Miserable	4.9118	2.1132
Neutral	4.1176	2.3191

Sample Sizes

The first calculations in this section all assume that there is an equal number of observations in each group
Unequal sample size calculations are covered later
We will refer to the number of observations in each group as n
The total number of observations as N
For these data there are four groups of 34 observations
Therefore n = 34 and N = 136

Computing MSE

The assumption of homogeneity of variance states that the variance within each of the populations (σ²) is the same
This variance, σ², is the quantity estimated by MSE and is computed as the mean of the sample variances
For these data, the MSE is equal to 2.6489

Computing MSB

The formula for MSB is based on the fact that the variance of the sampling distribution of the mean is

where n is the sample size. Rearranging this formula we have

Therefore, if we knew the variance of the sampling distribution of the mean, we could compute σ² by multiplying by n.
Although we do not know the variance of the sampling distribution of the mean, we can estimate it with the variance of the sample means. For the leniency data, the variance of the four sample means is 0.270
To estimate σ², we multiply the variance of the sample means (0.270) by n (the number of observations in each group, which is 34)
We find that MSB = 9.179.

To sum up these steps:

Compute the means
Compute the variance of the means
Multiply by the variance of the means by n

Recap

If the population means are equal, then both MSE and MSB are estimates of σ² and should therefore be about the same
Naturally, they will not be exactly the same since they are just estimates and are based on different aspects of the data:
- MSB is computed from the sample means
- MSE is computed from the sample variances.

If the population means are not equal, then MSE will still estimate σ² because differences in population means do not affect variances
However, differences in population means affect MSB since differences among population means are associated with differences among sample means
It follows that the larger the differences among sample means, the larger the MSB
In short, MSE estimates σ² whether or not the populations means are equal whereas MSB estimates σ² only when the population means are equal and estimates a larger quantity when they are not equal.

Comparing MSE and MSB

MSB estimates a larger quantity than MSE only when the population means are not equal
Therefore finding of a larger MSB than an MSE is a sign that the population means are not equal
MSB could be larger than MSE by chance even if the population means are equal
MSB must be much larger than MSE in order to justify the conclusion that the population means differ

But how much larger must MSB be?
For the Smiles and Leniency data, the MSB and MSE are 9.179 and 2.649 respectively
Is that difference big enough?
To answer, we would need to know the probability of getting this big a difference or a bigger difference between if the population means were all equal
The mathematics necessary to answer this question were worked out by the statistician Ronald Fisher

F Ratio

Although Fisher's original formulation took a slightly different form, the standard method for determining the probability is based on the ratio of MSB to MSE
This ratio is named after Fisher and is called the F ratio.

F = MSB/MSE

For these data, the F ratio is

F = 9.179/2.649 = 3.465

MSB is 3.465 times higher than MSE
Would this have been likely to happen if all the population means were equal?
That depends on the sample size
With a small sample size, it would not be too surprising because small samples are unreliable
However, with a very large sample, the MSB and MSE are almost always about the same, and an F ratio of 3.465 or larger would be very unusual

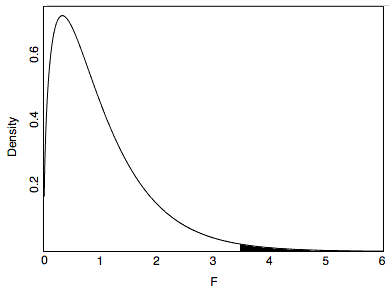Sampling distribution of F for the sample size in the Smiles and Leniency study

As you can see, it has a positive skew
For larger sample sizes, the skew is less

F distribution and interpretation

From the figure above you can see that F ratios of 3.465 or above are unusual occurrences
The area to the right of 3.465 represents the probability of an F that large or larger and is equal to 0.018
In other words, given the null hypothesis that all the population means are equal, the probability value is 0.018 and therefore the null hypothesis can be rejected
Therefore, the conclusion that at least one of the population means is different from at least on of the others is justified

F distribution and sample size

The shape of the F distribution depends on the sample size
More precisely, it depends on two degrees of freedom (df) parameters:
- one for the numerator (MSB)
- one for the denominator (MSE)

Recall that the degrees of freedom for an estimate of variance is equal to the number of scores minus one. Since the MSB is the variance of k means, it has k-1 df. The MSE is an average of k variances each with n-1 df. Therefore the df for MSE is k(n-1) = N-k where N is the total number of scores, n is the number in each group, and k is the number of groups. To summarize:

df_numerator   = k-1
df_denominator = N-k

For the Smiles and Leniency data,

dfnumerator   = k-1 = 4-1 = 3 
dfdenominator = N-k = 136-4 = 132
F = 3.465

The F distribution calculator shows that p = 0.018

One-Tailed or Two?

Is the probability value from an F ratio a one-tailed or a two-tailed probability?
In the literal sense, it is a one-tailed probability since, as you can see in figure above, the probability is the area in the right-hand tail of the distribution
However, the F ratio is sensitive to any pattern of differences among means
It is therefore a test of a two-tailed hypothesis and is best considered a two-tailed test.

Relationship to the t test

Both ANOVA and an independent-group t test can test the difference between two means
Results will always be the same
When there are only two groups the following relationship between F and t will always hold:

F(1,dfd) = t²(df)
 
dfd is the degrees of freedom for the denominator of the F test and
df is the degrees of freedom for the t test
dfd will always equal df.

Sources of Variation

Why do scores in an experiment differ from one another?
Consider the scores of two subjects in the Smiles and Leniency study:
- one from the "False Smile" condition
- one from the "Felt Smile" condition

Possible reasons that the scores could differ:

the subjects were treated differently (they were in different conditions and saw different stimuli)
the two subjects may have differed with regard to their tendency to judge people leniently
one of the subjects was in a bad mood after receiving a low grade on a test
innumerable other reasons

Unexplained Variance

All of these reasons except the first (subjects were treated differently) are possibilities that were not under experimental investigation and therefore all of differences (variation) due to these possibilities are unexplained

It is traditional to call unexplained variance error even though there is no implication that an error was made

Therefore, the variation in this experiment can be thought of as being either:

variation due to the condition the subject was in
due to error (the sum total of all reasons subjects's scores could differ that were not measured).

SSQ and GM

ANOVA partitions the variation into its various sources
The term sums of squares is used to indicate variation
The total variation is defined as the sum of squared differences from the mean of all subjects
The mean of all subjects is called the grand mean' and is designated as GM

= Sum of Squares Total

The total sum of squares (SSQ_total or SST) is defined as

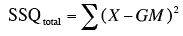
which means simply to take each score, subtract the grand mean from it, square the difference, and then sum up these squared values.

For the Smiles and Leniency study, SSQtotal = 377.19.

Sum of Squares Conditions

The sum of squares conditions is calculated as shown below:

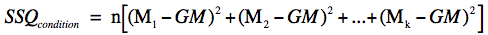
n is the number of scores in each group
k is the number of groups
M1 is the mean for Condition 1
M2 is the mean for Condition 2
M_k is the mean for Condition k

Smiles and Leniency study, the values are:

SSQ_condition = 34(5.37-4.83)² + (4.91-4.83)² + (4.91-4.83)² + (4.12-4.83)² = 27.5

If there are unequal sample sizes, the only change is that the following formula is used for the sum of squares for condition:

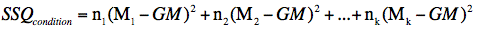
where ni is the sample size of the ith condition. SSQtotal is computed the same way as shown above.

Sum of Squares error

The sum of squares error is the sum of the squared deviations of each score from its group mean. This can be written as

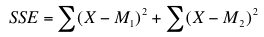
where Xi1 is the ith score in group 1 and M1 is the mean for group 1, Xi2 is the ith score in group 2 and M2 is the mean for group 2, etc

For the Smiles and Leniency study, the means are: 5.38, 4.91, 4.91, and 4.12. The SSQerror is therefore:

(2.5-5.38)² + (5.5-5.38)² + ... + (6.5-4.12)² = 349.66

The sum of squares error can also be computed by subtraction:

SSQerror = SSQtotal - SSQcondition
SSQerror = 377.19 - 27.53 = 349.66

Therefore, the total sum of squares of 3771.9 can be partitioned into SSQcondition (27.53) and SSQerror (349.66).

Once the sums of squares have been computed, the mean squares (MSB and MSE) can be computed easily. The formulas are:

MSB = SSQcondition/dfn

where dfn is the degrees of freedom numerator and is equal to k-1.

MSB = 27.5/3 = 9.17

which is the same value of MSB obtained previously (except for rounding error). Similarly,

MSE = SSQerror/dfd

where dfd is the degrees of freedom for the denominator and is equal to N-k

dfd = 136 - 4 = 132
MSE = 349.66/132 = 2.65

which is the same as obtained previously (except for rounding error) Note that the dfd are often called the dfe for degrees of freedom error.

The Analysis of Variance Summary Table

The table is a convenient way to summarize the partitioning of the variance

Source	df	SSQ	MS	F	p
Condition	3	27.5349	9.1783	3.465	0.0182
Error	132	349.6544	2.6489
Total	135	377.1893

Mean squares (MS) are always the sums of squares divided by degrees of freedom

Questions

Template:Statistics Links

One-Way Demo

simulations/anova1/anova1.html Template:Statistics Links

Multi-Factor ANOVA (Between-Subjects)

Learning Objectives

Define main effect, simple effect, interaction, and marginal mean
State the relationship between simple effects and interaction
Compute the source of variation and df for each effect in a factorial design
Plot the means for an interaction
Define three-way interaction

Basic Concepts and Terms

Bias Against Associates of the Obese Example

In the Bias Against Associates of the Obese case study, the researcher was interested in whether the weight of a companion of a job applicant would affect judgments of a male applicant's qualifications for a job
Two independent variables were investigated:
1. whether the companion was obese or of typical weight
2. whether the companion was a girl friend or just an acquaintance

One approach would have been to conduct two separate studies, one with each independent variable
However, it is more efficient to conduct one study that includes both independent variables
Moreover, there is a much bigger advantage than efficiency for including two variables in the same study:
it allows a test of the interaction between the variables.

Interation

There is an interaction when the effect of one variable differs depending on the level of a second variable
For example, it is possible that the effect of having an obese companion would differ depending on the relationship to the companion
Perhaps there is more prejudice against a person with an obese companion if the companion is a girl friend than if she is just an acquaintance
If so, there would be an interaction between the obesity factor and the relationship factor

Main Effect

There are three effects of interest in this experiment:

Weight: Are applicants judged differently depending on the weight of their companion?
Relationship: Are applicants judged differently depending on their relationship with their companion?
Weight x Relationship Interaction: Does the effect of weight differ depending on the relationship with the companion?

The first two effects (Weight and Relationship) are both main effects.
A main effect of an independent variable is the effect of the variable averaging over the levels of the other variable(s)

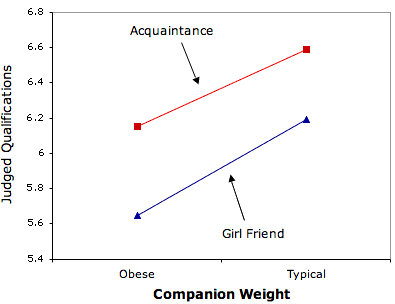
Marginal Means

It is convenient to talk about main effects in terms of marginal means
A marginal mean for a level of a variable is the mean of the means of all levels of the other variable

For example, the marginal mean for the level "Obese" is the average of "Girl-Friend-Obese" and "Acquaintance-Obese."

Table 1 shows that this marginal mean is equal to the average of 5.65 and 6.15 which is 5.90
Similarly, the marginal mean for Typical is the average of 6.19 and 6.59 which is 6.39
The main effect of Weight is based on a comparison of the these two marginal means
Similarly, the marginal means for Girl Friend and Acquaintance are 5.92 and 6.37.

Means for All Four Conditions
		Companion Weight
		Obese	Typical	Marginal Mean
Relationship	Girl Friend	5.65	6.19	5.92
Relationship	Acquaintance	6.15	6.59	6.37
	Marginal Mean	5.90	6.39

Simple Effect

The simple effect of a variable is the effect of the variable at a single level of another variable
The simple effect of "Weight" at the level of "Girl Friend" is the difference between the "Girl-Friend Typical" and the "Girl-Friend Obese" conditions
The difference is 6.19-5.65 = 0.54
Similarly, the simple effect of "Weight" at the level of "Acquaintance" is the difference between the "Acquaintance Typical" and the "Acquaintance Obese" conditions
The difference is 6.59-6.15 = 0.44.

Interaction and Simple Effect

There is an interaction when the effect of one variable differs depending on the level of another variable.
This is equivalent to saying that there is an interaction when the simple effects differ
In this example, the simple effects are 0.54 and 0.44
As shown below, these simple effects are not significantly different.

Tests of Significance

The important questions are not whether there are main effects and interactions in the sample data.
Instead, what is important is what the sample data allow you to conclude about the population
This is where Analysis of Variance comes it
ANOVA tests main effects and interactions for significance

ANOVA Summary Table
Source	df	SSQ	MS	F	p
Weight	1	10.4673	10.4673	6.214	0.0136
Relation	1	8.8144	8.8144	5.233	0.0234
W x R	1	0.1038	0.1038	0.062	0.8043
Error	172	289.7132	1.6844
Total	175	310.1818

Weight Analysis

Consider first the effect of "Weight."
The degrees of freedom (df) for "Weight" is 1
The degrees of freedom for a main effect is always equal to the number of levels of the variable minus one
Since there are two levels of the "Weight" variable (typical and obese) the df is 2 -1 = 1
The mean square (MS) is the sum of squares divided by the df
The F ratio is computed by dividing the MS for the effect by the MS for error (MSE)
For the effect of "Weight," F = 10.4673/1.6844 = 6.214
The last column, p, is is the probability of getting an F of 6.214 or larger given that there is no effect of weight in the population

The p value is 0.0136 which is quite low and therefore the null hypothesis of no main effect of "Weight" is rejected
The conclusion is that the weight of the companion lowers judgments of qualifications

Relation Analysis

The effect "Relation" is interpreted the same way
The conclusion is that being accompanied by a girl friend leads to lower ratings than being accompanied by an acquaintance.

Weight x Relation interaction

The df for an interaction is the product of the df of variables in the interaction
For the Weight x Relation interaction (W x R), the df = 1 since both Weight and Relation have one df: 1 x 1 = 1
The p value for the interaction is 0.8043 which is the probability of getting an interaction as big or bigger than the one obtained in the experiment if there were no interaction in the population
Therefore, these data provide no evidence for an interaction
Always keep in mind that the lack of evidence for an effect does not justify the conclusion that there is no effect
In other words, you do not accept the null hypothesis just because you do not reject it.

Error analysis

For "Error," the degrees of freedom is equal to the total number of observations minus the total number of groups
The sample sizes for this experiment are shown below
The total number of observations is 40 + 42 + 40 + 54 = 176
Since there are four groups, df = 176 - 4 = 172.

Sample Sizes for All Four Conditions
		Companion Weight
		Obese	Typical
Relationship	Girl Friend	40	42
Relationship	Acquaintance	40	54

Total Analysis

The final row is "Total."
The degrees of freedom total is equal to the sum of all degrees of freedom
It is also equal to the number of observations minus 1, or 176 -1 = 175
When there are equal sample sizes, the sum of squares total will equal the sum all other sums of squares
However, when there are unequal sample sizes, as there are here, this will not generally be true
The reasons for this are complex and are discussed in the section Unequal n .

Plotting Means

Although the plot shown below illustrates the main effects and the interaction (or lack of interaction) clearly, it is called an interaction plot
It is important to carefully consider the components of this plot
First, the dependent variable is on the Y axis
Second, one of the independent variables is on the X axis
In this case, it is the variable is "Weight."
Finally, a separate line is drawn for each level of the other independent variable
It is better to label the lines right on the graph as shown here than with a legend.

If you have three or more levels on the X axis, you should not use lines unless there is some numeric ordering to the levels
If your variable on the X axis is a qualitative variable, you can use a plot such as the one below
However, as discussed in the section on bar charts, it would be better to replace each bar with a box plot.

Line graphs are a common option with more than two levels if the variable is numeric
A line graph has the advantage of showing the pattern of interaction clearly
Its disadvantage is that it does not convey the distributional information contained in box plots.

An Example with Interaction

The following example was presented in the section on specific comparisons among means. It is also relevant here.

Twelve subjects were selected from a population of high-self-esteem subjects and an additional 12 subjects were selected from a population of low-self-esteem subjects
Subjects then performed on a task and (independent of how well they really did) half were told they succeeded and the other half were told they failed
Therefore there were six subjects in each esteem/success combination and 24 subjects altogether.

After the task, subjects were asked to rate (on a 10-point scale) how much of their outcome (success or failure) they attributed to themselves as opposed to being due to the nature of the task.

Data from Hypothetical Experiment on Attribution
		Esteem
		High	Low
Outcome	Success	7	6
		8	5
		7	7
		8	4
		9	5
		5	6
	Failure	4	9
		6	8
		5	9
		4	8
		7	7
		3	6

The ANOVA Summary Table for these data is shown in Table below.

ANOVA Summary Table for Made Up Data
Source	df	SSQ	MS	F	p
Outcome	1	0.0417	0.0417	0.0256	0.8744
Esteem	1	2.0417	2.0417	1.2564	0.2756
O x E	1	35.0417	35.0417	21.5641	0.0002
Error	20	32.5000	1.6250
Total	23	69.6250

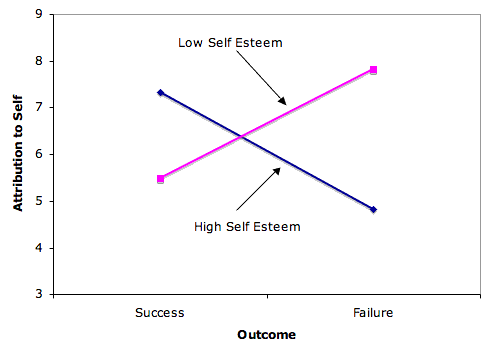
As you can see, the only significant effect is the Outcome x Esteem (O x E) interaction. The form of the interaction can be seen in Figure 5.

Clearly the effect of "Outcome" is different for the two levels of Esteem: For subjects high in self esteem, failure led to less attribution to oneself then did success.
By contrast, for subjects low in self esteem, failure led to more attribution to oneself than did success. Notice that the two lines in the graph are not parallel.

Nonparallel lines indicate interaction.

The significance test for the interaction determines whether it is justified to conclude that the lines in the population are not parallel.
Lines do not have to cross for there to be interaction.

Three-Factor Designs

Three-factor designs are analyzed in much the same way as two-factor designs
The table below shows the analysis of a study described by Franklin and Cooley investigating three factors on the strength of industrial fans:
1. Hole Shape (Hex or Round)
2. Assembly Type (Stake or Spun)
3. Barrel Shape (knurled or smooth)

The dependent variable, breaking torque, was measured in foot-pounds
There were eight observations in each of the eight combinations of the three factors.

As you can see in table below there are:

three main effect
three two-way interactions
one three-way interaction

The degrees of freedom for the main effects are, as in a two-factor design, equal to the number of levels of the factor minus one
Since all the factors here have two levels, all the main effects have one degree of freedom
The interaction degrees of freedom are always equal to the product of the degrees of freedom of the component parts
This holds for the three-factor interaction as well as the two-factor interactions
The error degrees of freedom is equal to the number of observations (64) minus the number of groups (8) and is 56.

ANOVA Summary Table for Fan Data
Source	df	SSQ	MS	F	p
Hole	1	8258.27	8258.27	266.68	<0.0001
Assembly	1	13369.14	13369.14	431.73	<0.0001
H x A	1	2848.89	2848.89	92.00	<0.0001
Barrel	1	35.0417	35.0417	21.5641	<0.0001
H x B	1	594.14	594.14	19.1865	<0.0001
A x B	1	135.14	135.14	4.36	0.0413
H x A x B	1	1396.89	1396.89	45.11	<0.0001
Error	56	1734.12	30.97
Total	63	221386.91

A three-way interaction means that the two-way interactions differ as a function of the level of the third variable
The usual way to portray a three-way interaction is to plot the two-way interactions separately
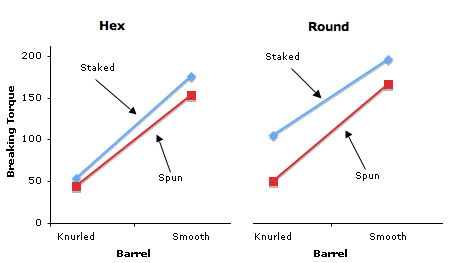
The Figure below shows the Barrel (knurled or smooth) x Assembly (Staked or Spun) separately for the two levels of Hole Shape (Hex or Round)
For the Hex Shape, there is very little interaction with the lines being close to parallel with a very slight tendency for the effect of Barrel to be bigger for Staked than for Spun
The two-way interaction for the Round Shape is different: The effect of Barrel is bigger for Spun than for Staked
The finding of a significant three-way interaction indicates that this difference in two-way interactions is not due to chance.

Questions

Data used to most of the questions:

Age	Recall	Score
1	1	9.0
1	2	7.0
1	3	11.0
1	1	8.0
1	2	9.0
1	3	13.0
1	1	6.0
1	2	6.0
1	3	8.0
1	1	8.0
1	2	6.0
1	3	6.0
1	1	10.0
1	2	6.0
1	3	14.0
1	1	4.0
1	2	11.0
1	3	11.0
1	1	6.0
1	2	6.0
1	3	13.0
1	1	5.0
1	2	3.0
1	3	13.0
1	1	7.0
1	2	8.0
1	3	10.0
1	1	7.0
1	2	7.0
1	3	11.0
2	1	8.0
2	2	10.0
2	3	14.0
2	1	6.0
2	2	7.0
2	3	11.0
2	1	4.0
2	2	8.0
2	3	18.0
2	1	6.0
2	2	10.0
2	3	14.0
2	1	7.0
2	2	4.0
2	3	13.0
2	1	6.0
2	2	7.0
2	3	22.0
2	1	5.0
2	2	10.0
2	3	17.0
2	1	7.0
2	2	6.0
2	3	16.0
2	1	9.0
2	2	7.0
2	3	12.0
2	1	7.0
2	2	7.0
2	3	11.0

	The effect of one variable at a single level of another variable.
	The effect of one variable on a single level of another variable.
	The smallest effect of a variable.
	The effect that is an even multiple of the main effect.

Answer >>

The effect of one variable at a single level of another variable.

	The effect of two variables is larger than the effect of one variable.
	The main effects are larger than the simple effects.
	The simple effects differ.
	The effect of one variable differs depending on the level of another variable.

Answer >>

The simple effects differ and The effect of one variable differs depending on the level of another variable.

Answer >>

The df is (4-1) x (2-1) equals 3.

Answer >>

0.0299

Answer >>

0.0299

Answer >>

4.5933

Answer >>

4.9758

Template:Statistics Links

Unequal Sample Sizes

Learning Objectives

State why unequal n can be a problem
Define confounding
Compute weighted and unweighted means
Distinguish between Type I and Type III sums of squares
Describe why the cause of the unequal sample sizes makes a difference for the interpretation

The Problem of Confounding

Whether by design, accident, or necessity, the number of subjects in each of the conditions in an experiment may not be equal.
For example, the sample sizes for the Obesity and Relationships case study are shown in table below
Although the sample sizes were approximately equal, the most subjects were in the Acquaintance/Typical condition
Since n is used to refer to the sample size of an individual group, designs with unequal samples sizes are sometimes referred to as designs with unequal n.

Sample Sizes for Obesity and Relationships
		Companion Weight
		Obese	Typical
Relationship	Girl Friend	40	42
Relationship	Acquaintance	40	54

An absurd design

We consider an absurd design to illustrate the main problem caused by unequal n.
Suppose an experimenter were interested in the effect of diet and exercise on cholesterol

Sample Sizes for Diet and Exercise
		Exercise
		Moderate	None
Diet	Low Fat	5	0
Diet	High Fat	0	5

What makes this example absurd, is that there are no subjects in either the Low Fat/No exercise condition or the High Fat/Moderate exercise condition

Data for Diet and Exercise
		Exercise
		Moderate	None	Mean
Diet	Low Fat	-20	0	-25
		-25
		-30
		-35
		-15
	High Fat	0	-20	-5
			6
			-10
			-6
			5
	Mean	-25	-5	-15

The last column shows the mean change in cholesterol for the two Diet conditions whereas the last row shows the mean change for the two Exercise conditions.
The value of -15 in the lower-right most cell in the table is the mean of all subjects.

We see from the last column that those on the low-fat diet lowered their cholesterol an average of 25 units whereas those on the high-fat diet lowered theirs by only 5 units
However, there is no way of knowing whether the difference is due to diet or to exercise since every subject in the low-fat condition was in the moderate-exercise condition and every subject in the high-fat condition was in the no-exercise condition
Therefore, Diet and Exercise are completely confounded.

The problem with unequal n is that it causes confounding.

Weighted and Unweighted Means

The difference between weighted and unweighted means is critical for understanding how to deal with the confounding resulting from unequal n.

Weighted and unweighted means will be explained using the data shown in Table 4
Here, Diet and Exercise are confounded because 80% of the subjects in the low-fat condition exercised as compared to 20% of those in the high-fat condition
However, there is not complete confounding as there was with the data in the Absurd Example

The weighted mean for "low fat" is computed as the mean of the low-fat moderate-exercise condition and the low-fat no-exercise mean, weighted in accordance with sample size
To compute a weighted mean, you multiply each mean by its sample size and divide by N, the total number of observations
Since there are four subjects in the low-fat moderate-exercise condition and one subject in the low-fat no-exercise condition, the means are weighted by factors of 4 and 1 as shown below where M_w is the weighted mean.

The weighted mean for the low-fat condition is also the mean of all five scores in this condition.
Thus if you ignore the factor "Exercise," you are implicitly computing weighted means.

The unweighted mean for the low-fat condition (M_u) is simply the mean of the two means.

Data for Diet and Exercise with Partial Confounding (Table 4)
		Exercise
		Moderate	None	Weighted Mean	Unweighted Mean
Diet	Low Fat	-20	-20	-26	-23.75
		-25
		-30
		-35
		M=-27.5	M=-20.0
	High Fat	-15	6	-4	-8.125
			-6
			5
			-10
		M=-15.0	M=-1.25
	Weighted Mean	-25	-5
	Unweighted Mean	-21.25	-10.625

One way to evaluate the the main effect of Diet is to compare the weighted mean for the low-fat diet (-26) with the weighted mean for the high-fat diet (-4)
This difference of -22 is called "the effect of diet ignoring exercise" and is misleading since most of the low-fat subjects exercised and most of the high-fat subjects did not
However, the difference between the unweighted means of -15.5 (-23.75 minus -8.25) is not affected by this confounding and is therefore a better measure of the main effect

In short:

the weighted means ignore the effects of other variables (exercise in this example) and result in confounding;
unweighted means control for the effect of other variables and therefore eliminate the confounding.

Statistical analysis programs use different terms for means that are computed controlling for other effects. SPSS calls them "estimated marginal means" whereas SAS and SAS JMP call them least squares means.

Types of Sums of Squares

The section on Multi-factor ANOVA stated that the sum of squares total was not equal to the sum of the sum of squares for all the other sources of variation when there is unequal n.
This is because the confounded sums of squares are not apportioned to any source of variation
For the data in Table 4:
- the sum of squares for Diet is 390.625
- the sum of squares for Exercise is 180.625
- the sum of squares confounded between these two factors is 819.375

Type III Sums of Squares

In the ANOVA Summary Table shown in Table 5, this large portion of the sum of squares is not apportioned to any source of variation and represents the "missing" sums of squares
That is, if you add up the sums of squares for Diet, Exercise, D x E, and Error, you get 904.625
If you add the confounded sum of squares of 819.375 to this value you get the total sum of squares of 1722.00
When confounded sums of squares are not apportioned to any source of variation, the sums of squares are called Type III sums of squares
Type III sums of squares are, by far, the most common and if sums of squares are not otherwise labelled, it can safely be assumed that they are Type III

ANOVA Summary Table for Type III SSQ (Table 5)
Source	df	SSQ	MS	F	p
Diet	1	390.625	390.625	7.43	0.034
Exercise	1	180.625	180.625	3.423	0.113
D x E	1	15.625	15.625	0.2969	0.605
Error	6	315.750	52.625
Total	9	1722.000

Type I Sums of Squares

When confounded sums of squares are apportioned to sources of variation, the sums of squares are called Type I sums of squares
The order in which the confounded sums of squares is apportioned is determined by the order in which the effects are listed
The first effect gets any sums of squares confounded between it and any of the other effects
The second gets the sums of squares confounded between it and subsequent effects, but not confounded with the first effect, etc
The Type I sums of squares are shown in Table 6
As you can see, with Type I sums of squares, the sum of all sums of squares is the total sum of squares.

ANOVA Summary Table for Type I SSQ (Table 6)
Source	df	SSQ	MS	F	p
Diet	1	1210.000	390.625	7.43	0.034
Exercise	1	180.625	180.625	3.423	0.113
D x E	1	15.625	15.625	0.2969	0.605
Error	6	315.750	52.625
Total	9	1722.000

Type II Sums of Squares

In Type II sums of squares, sums of squares confounded between main effects is not apportioned to any source of variation whereas sums of squares confounded between main effects and interactions is apportioned to the main effects
In our example, there is no confounding between D x E interaction and either of the main effects
Therefore, the Type II sums of squares are equal to the Type III sums of squares.

Unweighted Mean Analysis

Type III sums of squares are tests of difference in unweighted means
However, there is an alternative method to testing the same hypotheses tested using Type III sums of squares
This method, unweighted means analysis, is computationally simpler than the standard method but is an approximate test rather than an exact test
It is, however, a very good approximation in all but extreme cases
Moreover, it is exactly the same as the traditional test for effects with one degree of freedom

Causes of Unequal Samples

None of the methods for dealing with unequal sample sizes are valid if the experimental treatment is the source of the unequal sample sizes
Imagine an experiment seeking to determine whether publicly performing an embarrassing act would affect one's anxiety about public speaking
In this imaginary experiment, the experimental group is asked to reveal to a group of people the most embarrassing thing they have ever done
The control group is asked to describe what they had at their last meal
Twenty subjects are recruited for the experiment and randomly divided into two equal groups of 10, one for the experimental treatment and one for the control
Following the description, subjects are given an attitude survey concerning public speaking
This seems like a valid experimental design
However, of the 10 subjects in the experimental group, four withdrew from the experiment because they did not wish to publicly describe an embarrassing situation
None of the subjects in the control group withdrew
Even if the data analysis shows a significant effect, it would not be valid to conclude that the treatment had an effect because a likely alternative explanation cannot be ruled out
Namely, subjects who were willing to describe an embarrassing situation differed from those who were not even before the experiment began
Thus, the differential drop-out rate destroyed the random assignment of subjects to conditions, a critical feature of the experimental design
No amount of statistical adjustment can compensate for this flaw.

Questions

	The calculations are extremely difficult.
	The statistical results are only approximate.
	Unequal sample sizes result in confounding.
	Unequal sample sizes indicates a poor experimental design.

Answer >>

Unequal sample sizes causes confounding.

	Unweighted Means.
	Weighted Means.
	Correction for continuity.

Answer >>

Comparing unweighted means eliminates confounding.

	Type I Sums of squares.
	Type III Sums of squares.

Answer >>

Type III sums of squares test an effect while controlling for other effects thus eliminating confounding.

Template:Statistics Links

Tests Supplementing ANOVA

Learning Objectives

Compute Tukey HSD test
Describe an interaction in words
Describe why one might want to compute simple effect tests following a significant interaction

Tests Supplementing ANOVA

The null hypothesis tested in a one-factor ANOVA is that all the population means are equal
Stated more formally,

H0: μ1 = μ2 = ... μk
k is the number of conditions

When the null hypothesis is rejected, then all that can be said is that at least one population mean is different from at least one other population mean
The methods described in the sections on All Pairwise Comparisons and on Specific Comparisons for doing more specific tests apply here
Keep on mind that these tests are valid whether or not they are preceded by an ANOVA.

Main Effects

As shown below, significant main effects in multi-factor designs can be followed up in the same way as significant effects in a one-way designs
Table below shows the data from an imaginary experiment with three levels of Factor A and two levels of Factor B.

Made Up Example Data
	A1	A2	A3	Marginal Means
B1	5	9	7	7.08
	4	8	9
	6	7	9
	5	8	8
	Mean = 5	Mean = 8	Mean = 8.25
B2	4	8	8	6.50
	3	6	9
	6	8	7
	8	5	6
	Mean = 5.25	Mean = 6.75	Mean = 7.50
Marginal Means	5.125	7.375	7.875	6.79

Table below shows the ANOVA Summary Table for these data
The significant main effect of A indicates that, in the population, at least one of the marginal means for A is different from at least one of the others.

ANOVA Summary Table for Made Up Example Data
Source	df	SSQ	MS	F	p
A	2	34.333	17.17	9.29	0.0017
B	1	2.042	2.04	1.10	0.3070
AB	2	2.333	1.167	0.63	0.5431
Error	18	33.250	1.847
Total	23	71.958	3.129

Tukey HSD test

The Tukey HSD can be used to test all pairwise comparisons among means in a one-factor ANOVA as well as comparisons among marginal means in a multi-factor ANOVA.

The formula for the equal-sample-size case is shown below.


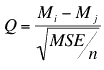Mi and Mj are marginal means
MSE is the mean square error from the ANOVA
n is the number of scores each mean is based upon

For this example, MSE = 1.847 and n= 8 because there are eight scores at each level of A
The probability value can be computed using the Studentized Range Calculator
The degrees of freedom is equal to the degrees of freedom error
For this example, df = 18
The results of the Tukey HSD test are shown in Table 3
The mean for A1 is significantly lower than the mean for A2 and the mean for A3
The means for A2 and A3 are not significantly different.

Pairwise Comparisons Among Marginal Means for A
Comparison	M_i - M_j	Q	p
A1 - A2	-2.25	-4.68	0.0103
A1 - A3	-2.75	-5.73	0.0021
A2 - A3	-0.50	-1.04	0.7456

Specific comparisons among means are also carried out much the same way as shown in the relevant section on testing means

The formula for L is


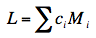ci is the coefficient for the ith marginal mean
Mi is the ith marginal mean

For example, to compare A1 with the average of A2 and A3, the coefficients would be 1, -0.5, -0.5

L = (1)(5.125) + (-0.5)(7.375) + (-0.5)(7.875) = -2.5

To compute t, use:


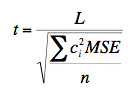= -4.25

MSE is the mean square error from the ANOVA
n is the number of scores each marginal mean is based on (eight in this example)

The degrees of freedom is the degrees of freedom error from the ANOVA and is equal to 18
Using the Online Calculator, we find that the two-tailed probability value is 0.0005
Therefore, the difference between A1 and the average of A2 and A3 is significant.

Important issues concerning multiple comparisons and orthogonal comparisons are discussed in the Specific Comparisons section in the Testing Means chapter.

Interactions

The presence of a significant interaction makes the interpretation of the results more complicated.
Since an interaction means that the simple effects are different, the main effect as the mean of the simple effects does not tell the whole story
This section discusses how to describe interactions, proper and improper uses of simple effects tests, and how to test components of interactions

Describing Interactions

A crucial step first step in understanding a significant interaction is constructing an interaction plot
Figure 1 shows an interaction plot from data presented in the section on Multi-factor ANOVA.

The second step is to describe the interaction in a clear and understandable way
This is often done by describing how by describing how the simple effects differed
Since this should be done using as little jargon as possible, the word "simple effect" need not appear in the description
An example is as follows:

The effect of Outcome differed depending on the subject's self esteem. 
The difference between the attributions to self following success and attributions to self following failure was   
larger for high-self-esteem subjects (mean difference = 2.50) 
than for low-self-esteem subjects (mean difference = -2.33).

No further analyses are helpful in understanding the interaction since the interaction means only that the simple effects differ
The interaction's significance indicates that the simple effects differ from each other, but provides no information about whether they differ from zero.

If neither simple effect is significant, the conclusion should be that the simple effects differ, and that at least one of them is not zero.
However, no conclusion should be drawn about which simple effect(s) is/are not zero.

Another error that can be made by mistakenly accepting the null hypothesis is to conclude that two simple effects are different because one is significant and the other is not
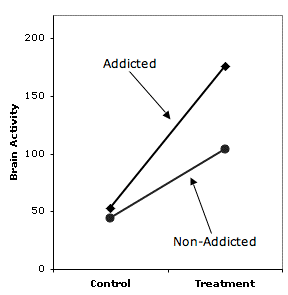
Consider the results of an imaginary experiment in which the researcher hypothesized that addicted people would show a larger increase in brain activity following some treatment than would non-addicted people
In other words, the researcher hypothesized that addiction status and treatment would interact
The results shown in Figure 2 are very much in line with the hypothesis
However, the test of the interaction resulted in a probability value of 0.08, a value not quite low enough to be significant at the conventional 0.05 level
The proper conclusion is that the experiment supports the researcher's hypothesis, but not strongly enough to allow a firm conclusion.

Simple Effect Tests

It is not necessary to know whether the simple effects differ from zero in order to understand an interaction because the question of whether simple effects differ from zero has nothing to do with interaction except that if they are both zero there is no interaction
It is not uncommon to see research articles in which the authors report that they analyzed simple effects in order to explain the interaction
However, this is not a correct since an interaction does not depend on the analysis of the simple effects.

However, there is a reason to test simple effects following a significant interaction
Since an interaction indicates that simple effects differ, it means that the main effects are not general
In the made-up example, the main effect of Outcome is not very informative, and the effect of outcome should be considered separately for high- and low-self-esteem subjects.

As will be seen, the simple effects of Outcome are significant and in opposite directions: Success significantly increases attribution to self for high-self-esteem subjects and significantly lowers attribution to self for low-self-esteem subjects
This is a very easy result to interpret.

What would the interpretation have been if neither simple effect had been significant?
On the surface, this seems impossible: How can the simple effects both be zero if they differ from each other significantly as tested by the interaction?
The answer is that a non-significant simple effect does not mean that the simple effect is zero: the null hypothesis should not be accepted just because it is not rejected

If neither simple effect is significant, the conclusion should be that the simple effects differ, and that at least one of them is not zero.
However, no conclusion should be drawn about which simple effect(s) is/are not zero.

Another error that can be made by mistakenly accepting the null hypothesis is to conclude that two simple effects are different because one is significant and the other is not. Consider the results of an imaginary experiment in which the researcher hypothesized that addicted people would show a larger increase in brain activity following some treatment than would non-addicted people. In other words, the researcher hypothesized that addiction status and treatment would interact. The results shown in Figure 2 are very much in line with the hypothesis. However, the test of the interaction resulted in a probability value of 0.08, a value not quite low enough to be significant at the conventional 0.05 level. The proper conclusion is that the experiment supports the researcher's hypothesis, but not strongly enough to allow a firm conclusion.

Unfortunately, the researcher was not satisfied with such a weak conclusion and went on to test the simple effects. It turned out that the effect of Treatment was significant for the Addicted group (p = 0.02) but not significant for the Non-Addicted group (p = 0.09). The researcher then went on to conclude that since there is an effect of Treatment for the Addicted group but not for the Non-Addicted group, the hypothesis of a greater effect for the former than for the latter group is demonstrated. This is faulty logic, however, since it is based on accepting the null hypothesis that the simple effect of Treatment is zero for the Non-Addicted group just because it is not significant.

Components of Interaction (optional)

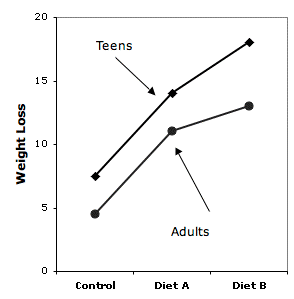
Figure 3 shows the results of an imaginary diet on weight loss. A control group and two diets were used for both overweight teens and overweight adults.

The difference between Diet A and the Control diet was essentially the same for teens and adults whereas the difference between Diet B and Diet A was much larger for the Teens than it was for the Adults. Over one portion of the graph the lines are parallel whereas over another portion they are not. It is possible to test these portions or components of interactions using the method of specific comparisons discussed previously. The test of the difference between Teens and Adults on the difference between Diets A and B could be tested with the coefficients shown in Table 4. Naturally, the same consideration regarding multiple comparisons and orthogonal comparisons apply to comparisons involving components of interaction that apply to other comparisons among means.

Coefficient for Component of the Interaction
Age Group	Diet	Coefficient
Teen	A	1
Teen	B	-1
Adult	A	-1
Adult	B	1

Questions

Template:Statistics Links

Within-Subjects ANOVA

Learning Objectives

Define a within-subjects factor
Explain why a within-subjects design can be expected to have more power than a between-subjects design
Be able to create the Source and df columns of an ANOVA summary table for a one-way within-subjects design
Explain error in terms of interaction
Discuss the problem of carry-over effects
Be able to create the Source and df columns of an ANOVA summary table for a design with one between-subjects and one within-subjects variable
Define sphericity
Describe the consequences of violating the assumption of sphericity
Discuss courses of action that can be taken if sphericity is violated

Within-Subjects

Within-subjects factors involve comparisons of the same subjects under different conditions
For example, in the ADHD Treatment Study, each child's performance was measured four times, once after being on each of four drug doses for a week
Therefore, each subject's performance was measured at each of the four levels of the factor "Dose."
Note the difference from between-subjects factors for which each subject's performance is measured only once and the comparisons are among different groups of subjects
A within-subjects factor is sometimes referred to as a repeated measures factor since repeated measurements are taken on each subject
An experimental design in which the independent variable is a within-subjects factor is called a within-subjects design.

One-factor Designs

ADHD Example

Let's consider how to analyze the data from the ADHD treatment case study
These data consist of the scores of 24 children with ADHD on a delay of gratification (DOG) task
Each child was tested under four dosage levels
For now we will be concerned only with testing the difference between the mean in the placebo condition (the lowest dosage, D0) and the mean in the highest dosage condition (D60)

ANOVA Summary Table
Source	df	SSQ	MS	F	p
Subjects	23	5781.98	251.39
Dosage	1	295.02	295.02	10.38	0.004
Error	23	653.48	28.41
Total	47	630.48

Results Interpretation

The first source of variation, "Subjects," refers to the differences among subjects
If all the subjects had exactly the same mean (across the two dosages) then the sum of squares for subjects would be zero; the more subjects differ from each other, the larger the sum of squares subjects.

Dosage refers to the differences between the two dosage levels
If the means for the two dosage levels were equal, the sum of squares would be zero
The larger the difference between means, the larger the sum of squares.
The error reflects the degree to which the effect of dosage is different for different subjects
If subjects all responded very similarly to the drug, then the error would be very low
For example, if all subjects performed moderately better with the high dose than they did with the placebo, then the error would be low
On the other hand, if some subjects did better with the placebo while others did better with the high dose, then the error would be high
It should make intuitive sense that the less consistent the effect of the drug, the larger the drug effect would have to be in order to be significant
The degree to which the effect of the drug differs depending on the subject is the Subjects x Drug interaction
Recall that an interaction occurs when the effect of one variable differs depending on the level of another variable
In this case, the size of the error term is the extent to which the effect of the variable "Drug" differs depending on the level of the variable "Subjects."
Note that each subject is a different level of the variable "Subjects."

Other portions of the summary table have the same meaning as in between-subjects ANOVA. The F for dosage is the mean square for dosage divided by the mean square error
For these data, the F is significant with p = 0.004. Notice that this F test is equivalent to the t-test for correlated pairs, with F = t2.

Design for four dosage level

Table 2 shows the ANOVA Summary Table when all four doses are included in the analysis
Since there are now four dosage levels rather than two, the df for dosage is three rather than one
Since the error is the Subjects x Dosage interaction, the df for error is the df for "Subjects" (23) times the df for Dosage (3) and is equal to 69.

ANOVA Summary Table
Source	df	SSQ	MS	F	p
Subjects	23	9065.49	394.15
Dosage	3	557.61	185.87	5.18	0.003
Error	69	2476.64	35.89
Total	95	12099.74

Carry-over effects

Often performing in one condition affects performance in a subsequent condition in such a way to make a within-subjects design impractical
For example, consider an experiment with two conditions
In both conditions subjects are presented with pairs of words
In Condition A subjects are asked to judge whether the words have similar meaning whereas in Condition B subjects are asked to judge whether they sound similar
In both conditions, subjects are given a surprise memory test at the end of the presentation
If condition were a within-subjects variable, then the there would be no surprise after the second presentation and it is likely that the subjects would have been trying to memorize the words.

Not all carry-over effects cause such serious problems
For example, if subjects get fatigued by performing a task, then they would be expected to do worse on the second condition they were in
However, as long as half the subjects are in Condition A first and Condition B second, the fatigue effect itself would not invalidate the results, although it would add noise and reduce power
The carryover effect is symmetric in that having Condition A first affects performance in Condition B to the same degree that having Condition B first affects performance in Condition A.

Asymmetric carryover effects cause more serious problems
For example, suppose performance in Condition B were much better if preceded by Condition A whereas performance in Condition A was approximately the same regardless of whether it was preceded by Condition B
With this kind of carryover effect it is probably better to use a between-subjects design.

One between and one-within-subjects factor

In the Stroop Interference case study, subjects performed three tasks: naming colors, reading color words, and naming the ink color of color words
Some of the subjects were males and some of the subjects were females
Therefore this design had two factors: gender and task
The ANOVA Summary Table for this design is shown in Table 3.

ANOVA Summary Table for Stroop Experiment
Source	df	SSQ	MS	F	p
Gender	1	83.32	83.32	1.99	0.165
Error	45	1880.56	41.79
Task	2	9525.97	4762.99	228.06	<0.001
Gender x Task	2	55.85	27.92	1.34	0.268
Error	90	1879.67	20.89

First notice that there are two error terms: one for the between-subjects variable Gender and one for both the within-subjects variable Task and the interaction of the between-subjects variable and the within-subjects variable
Typically, the mean square error for the between-subjects variable will be higher than the other mean square error
In this example, the mean square error for Gender is about twice as large as the other mean square error.

The degrees of freedom for the between-subjects variable is equal to the number of levels of the between subjects variable minus one
In this example it is one since there are two levels of gender. Similarly, the degrees of freedom for the within-subjects variable is equal to the number of levels of the variable minus one
In this example, it is two since there are three tasks
The degrees of freedom for the interaction is the product of the degrees of freedom of the two variables.
For the Gender x Task interaction, the degrees of freedom is the product of degrees of freedom Gender (which is 1) and the degrees of freedom Task (which is 2) and is equal to 2.

Assumption of Sphericity

Within-subjects ANOVA makes a restrictive assumption about the variances and the correlations among the dependent variables
Although the details of the assumption are beyond the scope of this book, it is approximately correct to say that it is assumed that all the correlations are equal and all the variances are equal
Table 4 shows the correlations among the three dependent variables in the Stroop Interference case study.

Correlations Among Variables
	word reading	color naming	interference
word reading	1	0.7013	0.1583
color naming	0.7013	1	0.2382
interference	0.1583	0.2382	1

Note that the correlation between the word reading and the color naming variables of 0.7013 is much higher than the correlation between either of these variables with the interference variable
Moreover, as shown in Table 5, the variances among the variables differ greatly.

Variances
Variable	Variance
word reading	15.77
color naming	13.92
Interference	55.07

Naturally, the assumption of sphericity, like all assumptions, refers to populations not samples
However it is clear from these sample data, the assumption is not met here in the population.

Consequences of Violating the Assumption of Sphericity

Although ANOVA is robust to most violations of its assumptions, the assumption of sphericity is an exception: Violating the assumption of sphericity leads to a substantial increase in the Type I error rate.
Moreover, this assumption is rarely met in practice
Although violations of this assumption had at one time received little attention, the current consensus of data analysts is that it is no longer considered acceptable to ignore them.

Approaches to Dealing with Violations of Sphericity

If an effect is highly significant, there is a conservative test that can be used to protect against an inflated Type I error rate
This test consists of adjusting the degrees of freedom for all within subject variables as follows: The degrees of freedom numerator and denominator are divided by the number of scores per subject minus one.
Consider the effect of Task shown in Table 3
There are three scores per subject and therefore the degrees of freedom should be divided by two
The adjusted degrees of freedom are:

(2)(1/2) = 1 for the numerator and
(90)(1/2)= 45 for the denominator

The probability value is obtained using the F probability calculator with the new degrees of freedom parameters
The probability of an F of 228.06 or larger with 1 and 45 degrees of freedom is less than 0.001
Therefore, there is no need to worry about the assumption violation in this case.
Possible violation of sphericity does make a difference in the interpretation of the analysis shown in Table 2.
The probability value of an F or 5.18 with 1 and 23 degrees of freedom is 0.032, a value that would lead to a more cautious conclusion than the p value of 0.003 shown in Table 2.

The correction described above is very conservative and should only be used when, as in Table 3, the probability value is very low
A better correction, but one that is very complicated to calculate is to multiply the degrees of freedom by a quantity called ε
There are two methods of calculating ε
The correction called the Huynh-Feldt (or H-F) is slightly preferred to the called the Geisser Greenhouse (or G-G) although both work well
The G-G correction is generally considered a little too conservative
A final method for dealing with violations of sphericity is to use a multivariate approach to within-subjects variables
This method has much to recommend it, but it is beyond the score of this text.

Questions

Template:Statistics Links

Power of Within-Subjects Designs Demo

power_within_demo.html Template:Statistics Links

	a. short, average
	b. basketball performance, average
	c. height, short
	d. childhood, adolescence
	e. age, child

	MSE/MSB is high.
	MSE/MSB = 1.
	MSB/MSE is low.
	MSB/MSE is high.

	Tukey's test.
	An interaction test.
	A specific comparison.
	ANOVA

	simple effects.
	pairwise comparisons.
	specific comparisons.
	main effects.

	Age: Subjects of four different ages were used in the experiment.
	Trials: Each subject had three trials on the task and their score was recorded for each trial.
	Dose: Each subject was tested under each of five dose levels.
	Days: Each subject was tested once a day for four days.
	Intensity: Each subject was randomly assigned to one of five intensity levels.

	Within-subjects
	Between-subjects
	Cannot be determined with the given information

	Neither MSB nor MSE can ever be a negative value.
	MSB is never less than 1.
	MSE is never less than 1.

	positive skew
	no skew
	negative skew