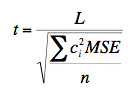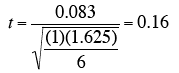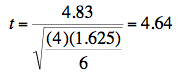Specific Comparisons (Independent Groups)
Learning Objectives
- Define linear combination
- Specify a linear combination in terms of coefficients
- Do a significance test for a specific comparison
Specific Comparisons (Independent Groups)
- There are many occasions on which the comparisons among means are more complicated than simply comparing one mean with another
- This section shows how to test these more complex comparisons.
- The methods in this section assume that the comparison among means was decided on before looking at the data (planned comparisons)
- A different procedure is necessary for unplanned comparisons
Self-esteem Example
- Twelve subjects were selected from a population of:
- high-self-esteem subjects (esteem = 1)
- an additional 12 subjects were selected from a population of low-self-esteem subjects (esteem = 2)
- Subjects then performed on a task and (independent of how well they really did) half were told they:
- succeeded (outcome = 1)
- the other half were told they failed (outcome = 2)
- Therefore there were six subjects in each esteem/success combination and 24 subjects altogether.
After the task, subjects were asked to rate (on a 10-point scale) how much of their outcome (success or failure) they attributed to themselves as opposed to being due to the nature of the task.
| outcome | esteem | attrib |
|---|---|---|
| 1 | 1 | 7 |
| 1 | 1 | 8 |
| 1 | 1 | 7 |
| 1 | 1 | 8 |
| 1 | 1 | 9 |
| 1 | 1 | 5 |
| 1 | 2 | 6 |
| 1 | 2 | 5 |
| 1 | 2 | 7 |
| 1 | 2 | 4 |
| 1 | 2 | 5 |
| 1 | 2 | 6 |
| 2 | 1 | 4 |
| 2Template:Statistics Links | 1 | 6 |
| 2 | 1 | 5 |
| 2 | 1 | 4 |
| 2 | 1 | 7 |
| 2 | 1 | 3 |
| 2 | 2 | 9 |
| 2 | 2 | 8 |
| 2 | 2 | 9 |
| 2 | 2 | 8 |
| 2 | 2 | 7 |
| 2 | 2 | 6 |
The means of the four conditions are shown in table below
| Outcome | Esteem | Mean |
|---|---|---|
| Success | High Self Esteem | 7.333 |
| Low Self Esteem | 5.500 | |
| Failure | High Self Esteem | 4.833 |
| Low Self Esteem | 7.833 |
Does positive outcome boost self-esteem?
- Did, on average, subjects who were told they succeeded differed significantly from subjects who were told they failed?
- The means for subjects in the success condition are 7.333 for the high-self-esteem subjects and 5.500 for the low-self-esteem subjects
The mean of all subjects in the:
- success condition is (7.333 + 5.500)/2 = 6.417
- failure condition is (4.833 + 7.833)/2 = 6.333
How do we do a significance test for this difference of 6.417-6.333 = 0.083?
Linear Combination
The first step is to express this difference in terms of a linear combination of a set of coefficients and the means We can compute the mean of the success and failure conditions:
Msuccess = (.5)(7.333) + (.5)(5.500) = 6.42 Mfailure = (.5)(4.833) + (.5)(7.833) = 6.33
The difference between the two means can be expressed as
.5 x 7.333 + .5 x 5.500 -(.5 x 4.833 + .5 x 7.833) = .5 x 7.333 + .5 x 5.500 -.5 x 4.833 - .5 x 7.83
- We therefore can compute the difference between the "success" mean and the "failure" mean by multiplying each "success" mean by 0.5, each failure mean by -0.5 and adding the results
- In Table below, the coefficient column is the multiplier and the product column in the result of the multiplication.
- If we add up the four values in the product column we get
L = 3.667 + 2.750 - 2.417 - 3.917 = 0.083
- This is the same value we got when we computed the difference between means previously (within rounding error)
- We call the value "L" for "linear combination."
| Outcome | Esteem | Mean | Coeff | Product |
|---|---|---|---|---|
| Success | High Self Esteem | 7.333 | 0.5 | 3.667 |
| Low Self Esteem | 5.500 | 0.5 | 2.750 | |
| Failure | High Self Esteem | 4.833 | -0.5 | -2.417 |
| Low Self Esteem | 7.833 | -0.5 | -3.917 |
Now, the question is whether our value of L is significantly different from 0. The general formula for L is:
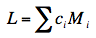
where ci is the ith coefficient and Mi is the ith mean. As shown above, L = 0.083. The formula for testing L for significance is shown below
MSE is the mean of the variances. The four variances are shown in the table below. Their mean is 1.625. Therefore MSE = 1.625.
| Outcome | Esteem | Variance |
|---|---|---|
| Success | High Self Esteem | 1.867 |
| Low Self Esteem | 1.100 | |
| Failure | High Self Esteem | 2.167 |
| Low Self Esteem | 1.367 |
The value of n is the number of subjects in each group. Here, n = 6. Putting it all together,
The degrees of freedom is
df = N - k N is the total number of subjects (24) k is the number of groups (4) df = 20
We find that the two-tailed probability value is 0.874
Therefore, the difference between the "success" condition and the "failure" condition is not significant.
Does the effect of outcome (success or failure) differs depending on the self esteem of the subject?
- Does the effect of outcome (success or failure) differs depending on the self esteem of the subject?
- For example, success may make high-self-esteem subjects more likely to attribute the outcome to themselves whereas success may make low-self-esteem subjects less likely to attribute the outcome to themselves.
- First, we have to test a difference between differences
- Specifically, is the difference between success and failure outcomes for the high-self-esteem subjects different from the difference between success and failure outcomes for the low-self-esteem subjects
- The means shown in the table below show that this is the case
- For the high-self-esteem subjects, the difference between the success and failure is 7.333-4.8333 = 2.5
- For low-self-esteem subjects, the difference is 5.500-7.833=-2.333
- The difference between differences is 2.5 - (-2.333) =4.83.
| Self Esteem | Outcome | Mean | Coeff | Product |
|---|---|---|---|---|
| High | Success | 7.333 | 1 | 7.333 |
| Failure | 4.833 | -1 | -4.833 | |
| Low | Success | 5.500 | -1 | -5.500 |
| Failure | 7.833 | 1 | 7.833 |
To continue the calculations,
- The two-tailed p value is 0.0002
- Therefore, the difference between differences is highly significant.
Interaction
- In Analysis of Variance section, you will see that comparisons such as this are testing what is called an interaction
- In general, there is an interaction when the effect of one variable differs as a function of the level of another variable
- In this example the effect of the outcome variable is different depending on the subject's self esteem
- For the high-self-esteem subjects, success led to more self attributions than did failure; for the low-self-esteem subjects, success led to less self attributions than failure
Multiple Comparisons
- The more comparisons you make, the greater your chance of a Type I error
- It is useful to distinguish between two error rates:
- the per-comparison error rate and
- the familywise error rate.
Per Comparison Error Rate
- The per-comparison error rate is the probability of a Type I error for a particular comparison.
- The familywise error rate is the probability of making one or more Type I error in a family or set of comparisons.
In the attribution experiment discussed above, we computed two comparisons. If we use the 0.05 level for each comparison, then the per-comparison rate is simply 0.05.
Bonferroni inequality
- The family-wise rate can be complex
- There is a simple approximation that is fairly accurate when the number of comparisons is small
Let us define:
- α as the per-comparison error rate
- c as the number of comparisons
The following inequality always holds true for the familywise error rate (FW) can be approximated as:
FW ≤ cα
- This inequality is called the Bonferroni inequality.
Bonferroni correction
- The Bonferroni inequality can be used to control the familywise error rate as follows:
If you want to the familywise error rate to be α, you use α/c as the per-comparison error rate
- This correction, called the Bonferroni correction, will generally result in a family wise error rate less than α
Should the familywise error rate be controlled?
- Unfortunately, there is no clear-cut answer to this question.
- The disadvantage of controlling the familywise error rate is that it makes it more difficult to obtain a significant result for any given comparison: The more comparisons you do, the lower the per-comparison rate must be and therefore the harder it is to reach significance.
- That is, the power is lower when you control the familywise error rate.
- The advantage is that you have a lower chance of making a Type I error.
Family of comparisons
- One consideration is the definition of a family of comparisons
- Let's say you conducted a study in which you were interested in whether there was a difference between male and female babies in the age at which they started crawling
- After you finished analyzing the data, a colleague of yours had a totally different research question: Do babies who are born in the winter differ from those born in the summer in the age they start crawling?
- Should the familywise rate be controlled or should it be allowed to be greater than 0.05?
- Our view is that there is no reason you should be penalized (by lower power) just because your colleague used the same data to address a different research question.
- Therefore, the familywise error rate need not be controlled
- Consider the two comparisons done on the attribution example at the beginning of this section:
These comparisons are testing completely different hypotheses. Therefore, controlling the familywise rate is not necessary.

Now consider a study designed to investigate the relationship between various variables and the ability of subjects to predict the outcome of a coin flip.
- One comparison is between males and females;
- Second comparison is between those over 40 and those under 40
- Third is between vegetarians and non-vegetarians
- Fourth is between firstborns and others
The question of whether these four comparisons are testing different hypotheses depends on your point of view.
On the one hand, there is nothing about whether age makes a difference that is related to whether diet makes a difference
In that sense, the comparisons are addressing different hypotheses
On the other hand, the whole series of comparisons could be seen as addressing the general question of whether anything affects the ability to predict the outcome of a coin flip
If nothing does, then allowing the familywise rate to be high means that there is a high probability of reaching the wrong conclusion.
Orthogonal Comparisons
- In the preceding sections, we talked about comparisons being independent
- Independent comparisons are often called orthogonal comparisons
- There is a simple test to determine whether two comparisons are orthogonal:
If the sum of the products of the coefficients is 0, then the comparisons are orthogonal
- Consider again the experiment on the attribution of success or failure.
- The table below shows the coefficients previously presented in chapter
- Note that the sum of the numbers in this column is 0
- Therefore, the two comparisons are orthogonal.
| Outcome | Esteem | C1 | C2 | Product (C1 * C2) |
|---|---|---|---|---|
| Success | High Self Esteem | 0.5 | 1 | 0.5 |
| Low Self Esteem | 0.5 | -1 | -0.5 | |
| Failure | High Self Esteem | -0.5 | -1 | 0.5 |
| Low Self Esteem | -0.5 | 1 | -0.5 |
Non-orthogonal comparisons
- The table below shows two comparisons that are not orthogonal
- The first compares the high-self-esteem subjects to low-self-esteem subjects; the second considers only those in the success group compares high-self-esteem subjects to low-self-esteem subjects
- The failure group is ignored by using 0's as coefficients
- Comparison of these two groups of subjects for the whole sample is not independent of the comparison of them for the success group
- You can see that the sum of the products of the coefficients is 0.5 and not 0.
| Outcome | Esteem | C1 | C2 | Product (C1 * C2) |
|---|---|---|---|---|
| Success | High Self Esteem | 0.5 | 0.5 | 0.25 |
| Low Self Esteem | -0.5 | -0.5 | 0.25 | |
| Failure | High Self Esteem | 0.5 | 0.0 | 0.0 |
| Low Self Esteem | -0.5 | 0.0 | 0.0 |
Questions