Variance Sum Law I

There are many occasions in which it is important to know the variance of the sum of two variables.

• Consider the following situation:

1. you have two populations,
2. you sample one number from each population, and
3. you add the two numbers together.

• The question is, "What is the variance of this sum?"

Memory Span Example

• Suppose the two populations are the populations of 8-year-old males and 8-year-old females in Houston, Texas, and that the variable of interest is memory span.
• You repeat the following steps thousands of times:

1. sample one male and one female,
2. measure the memory span of each, and
3. sum the two memory spans.

• After you have done this thousands of times, you compute the variance of the sum.

• The variance of this sum can be computed according to the following formula:

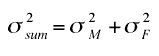where the first term is the variance of the sum, 
the second term is the variance of the males and 
the third term is the variance of the females. 

• Therefore, if the variances on the memory span test for the males and females were 0.9 and 0.8 respectively, then the variance of the sum would be 1.7.

• The formula for the variance of the difference between the two variables (memory span in this example) is shown below.
• Notice that the expression for the difference is the same as the formula for the sum.

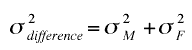
More generally, the variance sum law can be written as follows:

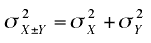which is read: The variance of X plus or minus Y is equal to 
the variance of X plus the variance of Y.

These formulas for the sum and difference of variables given above only apply when the variables are independent.

• We have thousands of randomly-paired scores.
• Since the scores are paired randomly, there is no relationship between the memory span of one member of the pair and the memory span of the other.
• Therefore, the two scores are independent.
• Contrast this situation with one in which thousands of people are sampled and two measures (such as verbal and quantitative SAT) are taken from each.
• In this case, there would be a relationship between the two variables since higher scores on the verbal SAT are associated with higher scores on the quantitative SAT (although there are many examples of people who score high on one test and low on the other).
• Thus the two variables are not independent and the variance of the total SAT score would not be the sum of the variances of the verbal SAT and the quantitative SAT.

Quiz

1 You have two populations. One has a mean of 4 and a variance of 2. The other has a mean of 5 and a variance of 4. You randomly draw one number from each of the populations and compute the sum. If you did this over and over again, what would be the variance of the sums?

Answer >>

6

2 +4 is 6

2 You have two populations. One has a standard deviation of 6. The other has a standard deviation of 8. You randomly draw one number from each of the populations and compute the sum. If you did this over and over again, what would be the standard deviation of the sums?

Answer >>

10

(6²)+(8²) is 100, The square root of 100 is 10

3 You know the variance of the midterm and the variance of the final in an English class. Can you calculate the variance of the sum with the information covered in this section?

	Yes
	No

Answer >>

No, because scores on the midterm and the final scores are not independent. This section only describes how to calculate the variance of the sum when the scores are independent.