Statistics for Decision Makers - 33.01 - Forecasting

title

33.01 - Forecasting

author

Bernard Szlachta (NobleProg Ltd) bs@nobleprog.co.uk

Economists。

There are two types of economists:

• those who don't know how to forecast interest rates
• and those who think they know how to forecast interest rates

What is Forecasting。

• Forecasting is the process of making statements about events whose actual outcomes have not yet been observed.
• Usually related to estimation for some variable of interest at some specified future date
• Prediction is a similar, but more general term

What forecast is not。

Target

A description of where we think we are heading, based on current assumptions

Plan

A set of future actions designed to reach an objective

Budget

A sum of money allocated to an activity or action to which an organization has committed itself

Two kind of Forecasting Models。

Momentum Forecasting Models

• We can predict, but our action will not change the assumptions of the forecast
• Usually mathematical or statistical models
• E.g. solar activity

Interventions Forecasting Models

• We try to asses the future in order to make decisions which in turn can usually prevent the forecast from happening
• Most of these forecasts are based on judgement
• There is feedback, i.e. the forecast itself changes the future (e.g. if you don’t change course, you will hit an iceberg)

Cassandra。

Cassandra was a daughter of the King of Troy She possessed the gift of prophecy She also refused Apollo's romantic advances He cursed her by making people ignore her warnings She predicted that Troy would fall to Greeks She warned about the "Trojan Horse" She was ignored, so we know that her predictions were right

Cassandra paradox 。

Don't confuse the Cassandra Paradox with Cassandra Syndrome

• Had the Trojans not ignored Cassandra would her prediction have been correct?

Raise your hand if you think her prediction would have been correct?

Business Point of View。

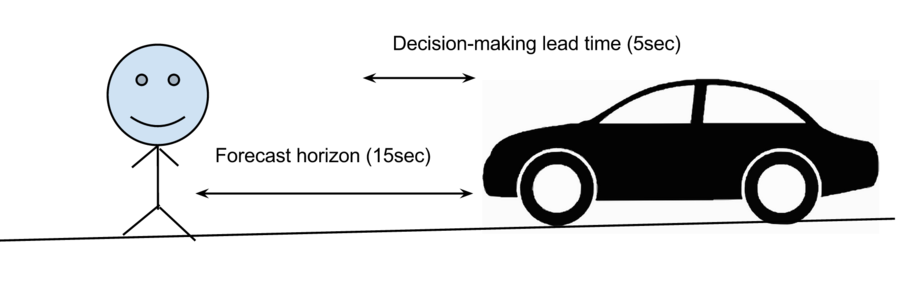
Decision-making lead time

The time between taking a decision to do something and the impact being manifested

Forecast horizon

The period of time in the future covered by a forecast

Implications

If the Decision-making lead time is longer than Forecast horizon, do not bother forecasting

Chaos Theory 。

• Deals with dynamical systems that are highly sensitive to initial conditions
• AKA the butterfly effect
• The system can be fully deterministic (as oppose to probabilistic), but can look random
• Managers should recognize the differences between probabilistic, deterministic and chaotic systems
• E.g. organization itself is considered chaotic

Lyapunov time。

• The Lyapunov time is the limit of the predictability of the system
• Examples of the Lyapunov time (without rare events)
  • Solar system: 50 million years
  • Pluto's orbit: 20 million years
  • Organization: from 1 day to hundreds of years
  • Scrum Team: 1 day to 30 days
  • Hydrodynamic chaotic oscillations: 2 seconds

What is a Model。

• A model is a simplified representation of the world
• Complex models are not usually "better"

Models。

Mathematical

• E.g. Revenue = Volume * Price
• If we increase speed from 100km/hour to 200km/hour for the train, the travel time will be reduced by 50%

Statistical

• Regression, Neural Networks, etc...
• People who study 30 mins more per day, with a 95% confidence level, achieve around 20% better results on average

Judgemental (gut feeling)

• E.g. "I think the recession will last 2 years longer"
• E.g. "Inflation will be around 2% next year"

Some Concepts 。

Risk and Uncertainty

Risk

Any deviation from a central forecast where the probability of occurrence can be estimated with a degree of confidence

Uncertainty

Any possible deviation from a central forecast where the probability of occurrence cannot be estimated with a degree of confidence

Central vs Range Forecast

Central forecast

The "single point" forecast

Range forecast

The estimated range of possible outcomes

What to forecast。

Simplest way of forecasting 。

Important Assumption

The future will look like the past (no discontinuity happened!)

Simple mean forecast

• The next customer will spend around £2000 (mean of previous purchases per customer)
• Usually a very big error of forecast (proportional to variance)

Naive forecast

• Very low error (e.g. stock exchange prices)
• The exchange rate of USD/GBP will be as it was yesterday

Regression model。

A relationship between a dependent variable and one or more independent variables.

E(Y | X) = f(X, β)

• The unknown parameters are denoted as β; this may be a scalar or a vector
• The independent variables, X
  • AKA: covariate, explanatory, predictor, control variable
  • The dependent variable, Y

Regression Assumptions 。

• The sample is representative of the population for the inference prediction
• The error is a random variable with a mean of zero conditional on the explanatory variables
• The independent variables are measured with no error
• The predictors are linearly independent, i.e. it is not possible to express any predictor as a linear combination of the others. See Multicollinearity.
• The errors are uncorrelated
• The variance of the error is constant across observations (homoscedasticity)
• If not, weighted least squares or other methods might instead be used

Types of Regression 。

Shape of the function

• Linear
• Non-linear

Number of predictors

• Simple (one predictor)
• General Multiple Regression

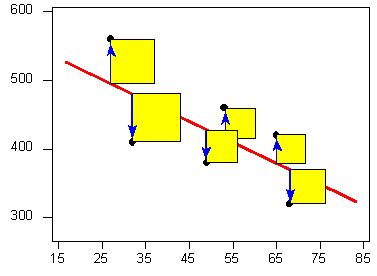
Ordinary Least Square 。

• Finds the line which minimizes squared distance scores from the line
• Uses calculus

Moving Average 。

The moving average is the plot line connecting all the (fixed) averages

• The moving average smooths the price data to form a trend following the indicators
• They do not predict the price direction, but rather define the current direction with a lag

Types

• Simple Moving Average (SMA)
• Exponential Moving Average (EMA)

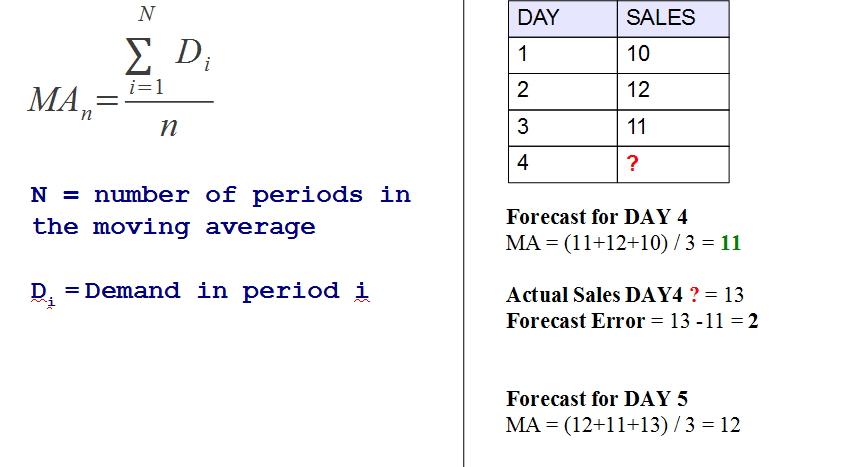
Simple Moving Average (SMA) 。

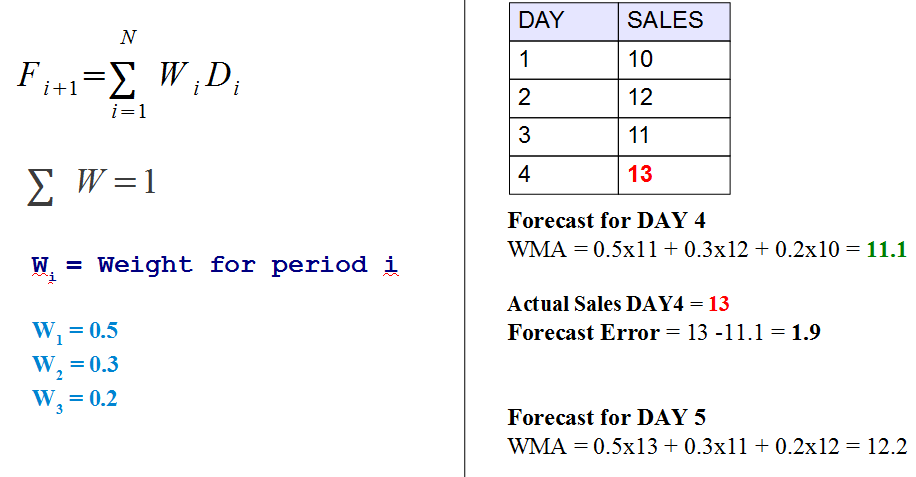
Weighted Moving Average (WMA) 。

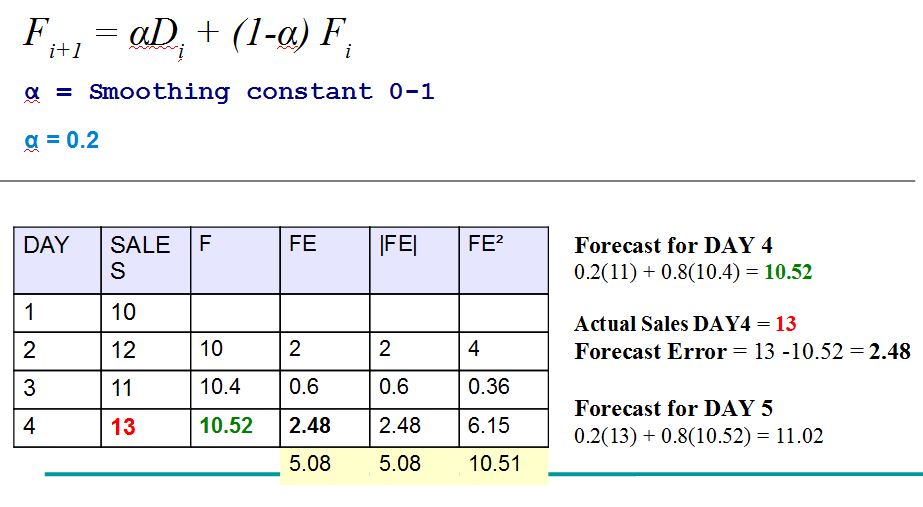
Exponential Smoothing 。

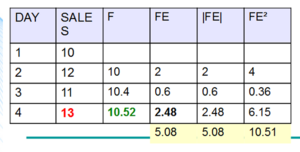
Forecast Error Measures。

Forecast Error Measures 。

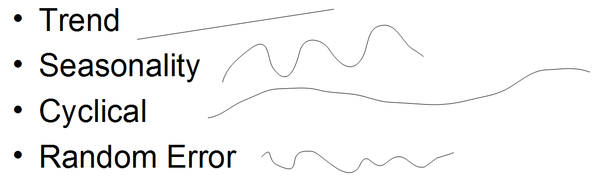
Time Series 。

• The data consist of a systematic pattern (usually a set of identifiable components) and random noise (error)
• Can be described in terms of two basic classes of components: trend and seasonality

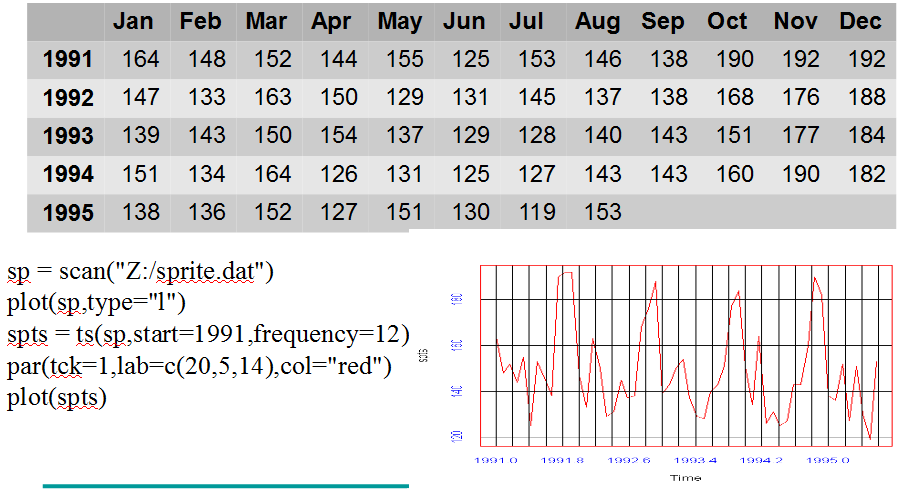
Forecasting Exercises - Sprite Sales 。

Code to paste

sp = scan("Z:/sprite.dat")
plot(sp,type="l")
spts = ts(sp,start=1991,frequency=12)
par(tck=1,lab=c(20,5,14),col="red")
plot(spts)

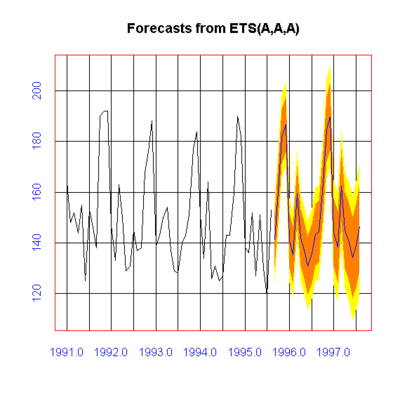
Forecasting ETS。

fc = forecast(spts)
print(fc)
plot(fc)
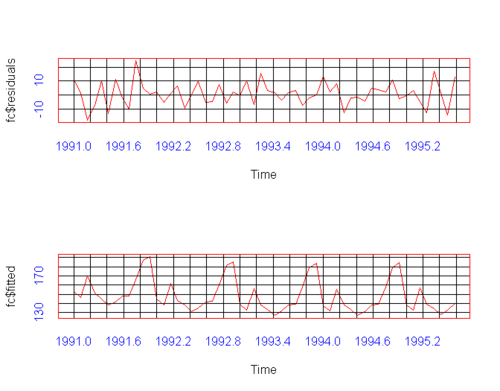
plot(fc$residuals)
lines(fc$fitted)

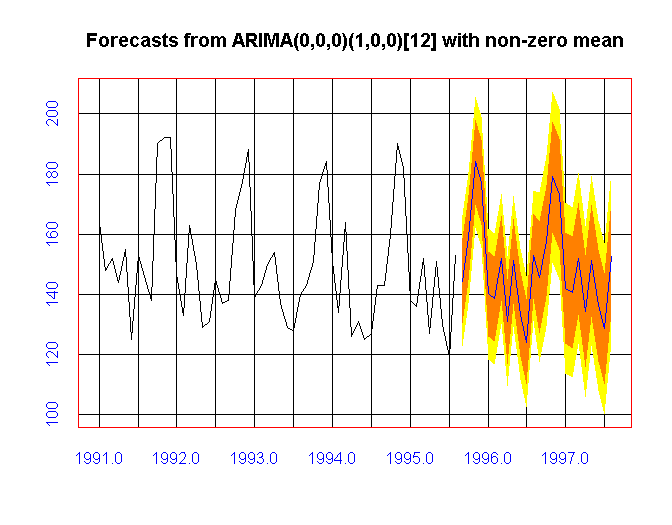
What are the sales of Sprite in Jan 1997 going to be? (Give range and point estimation)

ARIMA (auto)。

ar = auto.arima(spts)
fc = forecast(ar)
plot(fc)

Trend Analysis 。

• Smoothing involves some form of local averaging of data such that the nonsystematic components of individual observations cancel each other out
• The most common technique is moving average (mean or median)
• Fitting a function (usually linear)

Detrending and ensemble methods。

More: R - Time Series

Judgemental Methods。

• Surveys
• Delphi method
• Scenario building
• Technology forecasting
• Forecast by analogy

Combining Models。

• Usually we use all models (Judgemental + Statistical + Mathematical)
• For example, if we want to predict the revenue, we have price and volume
• Price * volume (mathematical model)
• Finding trends and analysis of seasonality (statistical)
• Scenario for growth - trend slope = 0, slope = 0.2, slope = 0.5
• Multiple models can be used and compared which delivers the best results (smallest error or prediction), it is referred to as an ensemble model