Statistics for Decision Makers - 14.06 - Regression - Non-linear Regression
Jump to navigation
Jump to search
<slideshow style="nobleprog" headingmark="。" incmark="…" scaled="false" font="Trebuchet MS" footer="www.NobleProg.co.uk" subfooter="Training Courses Worldwide">
- title
- 14.06 - Regression - Non-linear Regression
- author
- Bernard Szlachta (NobleProg Ltd) bs@nobleprog.co.uk
</slideshow>
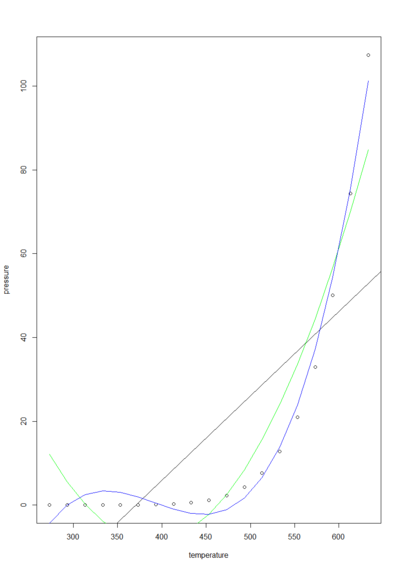
Non Linear Regression。
p <- read.csv("http://training-course-material.com/images/4/4f/Pressure.txt",h=T)
options(show.signif.stars=F)
m1 <- lm(pressure ~ temperature, data=p)
plot(p)
abline(m1)
summary(m1)
m2 <- lm(pressure ~ temperature + I(temperature^2), data=p)
lines(p$temperature,predict(m2),col="green")
summary(m2)
m3 <- lm(pressure ~ temperature + I(temperature^2) + I(temperature^3), data=p)
lines(p$temperature,predict(m3),col="blue")
summary(m3)
Non Linear Regression。
Nonlinear Regression model output 。
- m1
lm(formula = pressure ~ temperature, data = p)
Estimate Std. Error t value Pr(>|t|)
(Intercept) -74.7835 19.6282 -3.810 0.001400
temperature 0.2016 0.0421 4.788 0.000171
Multiple R-squared: 0.5742, Adjusted R-squared: 0.5492
p-value: 0.000171
- m2
lm(formula = pressure ~ temperature + I(temperature^2), data = p)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.272e+02 4.229e+01 5.373 6.22e-05
temperature -1.214e+00 1.941e-01 -6.255 1.15e-05
I(temperature^2) 1.562e-03 2.129e-04 7.336 1.67e-06
Multiple R-squared: 0.9024, Adjusted R-squared: 0.8902
p-value: 8.209e-09
- m3
lm(formula = pressure ~ temperature + I(temperature^2) + I(temperature^3),data = p)
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.758e+02 6.580e+01 -7.232 2.92e-06
temperature 3.804e+00 4.628e-01 8.219 6.16e-07
I(temperature^2) -9.912e-03 1.050e-03 -9.442 1.06e-07
I(temperature^3) 8.440e-06 7.703e-07 10.957 1.48e-08
Multiple R-squared: 0.9892, Adjusted R-squared: 0.987
p-value: 5.889e-15
Nonlinear Regression model output 。
Adjusted R2。
- Adjusted R2 is AKA , "R bar squared"
- Adjusted R2 spuriously increases when extra explanatory variables are added to the model
- Adjusted R2 >= R2
- It penalizes for more predictor variables
Model over-fitting。
- The polynomial function passes through each data point (if the number of the coefficients matches the number of points less one)
- If regression curves had been used to extrapolate the data, the overfit would have a bigger error of prediction
- The over-fitted model has less predictive power
Quiz …。
In all cases, the higher the R2 the better: True or False?
- False