Statistics for Decision Makers - 14.05 - Regression - Multiple Regression

title

14.05 - Regression - Multiple Regression

author

Bernard Szlachta (NobleProg Ltd) bs@nobleprog.co.uk

Introduction to Multiple Regression。

• Simple linear regression - one predictor variable
• Multiple regression - two or more predictor variables

Example

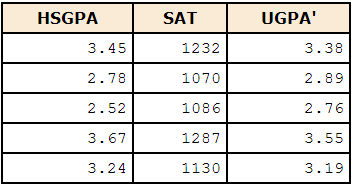
We want to predict a student's university grade point average (UGPA) on the basis of their High-School GPA (HSGPA) and their total SAT score

• We try find a linear combination of HSGPA and SAT that best predicts University GPA (UGPA)
• I.e. find the values of b1 and b2 in the equation shown below that give the best predictions of UGPA (OLS)

UGPA' = b1 x HSGPA + b2 x SAT + A
where UGPA' is the predicted value of University GPA 
A is a constant
b1, b2 are regression coefficients or regression weights

In this case:
UGPA' = 0.541 x HSGPA + 0.008 x SAT + 0.540

Multiple Correlation。

The multiple correlation (R) is equal to the correlation between the predicted scores and the actual scores

In this example, it is the correlation between UGPA' and UGPA

R = 0.79 
R is always positive

Assumptions。

• No assumptions are necessary for computing the regression coefficients
• Moderate violations of Assumptions 1-3 do not pose a serious problem for testing the significance of predictor variables
• Even small violations pose problems for confidence intervals

Assumptions

1. Errors (Residuals) are normally distributed
2. Variance is the same across all scores (Homoscedasticity)
3. Relationship is linear

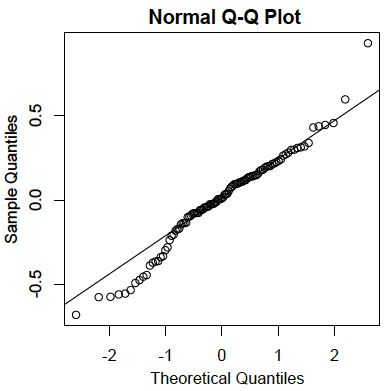
Residuals are normally distributed。

• The residuals are the errors of prediction
• They are the differences between the actual scores on the criterion and the predicted scores
• The plot below reveals that the actual data values at the lower end of the distribution do not increase as much as would be expected for a normal distribution
• It also reveals that the highest value in the data is higher than would be expected for the highest value in a sample of this size from a normal distribution
• Nonetheless, the distribution does not deviate greatly from normality

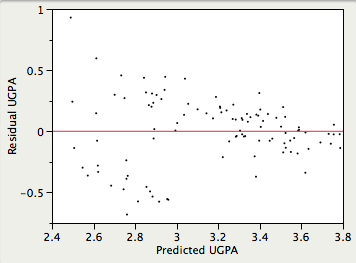
Homoscedasticity。

It is assumed that the variances of the errors of prediction are the same for all predicted values

Violation Example

• The errors of prediction are much larger for observations with low-to-medium predicted scores than for observations with high predicted scores
• A confidence interval on a low predicted UGPA would underestimate the uncertainty

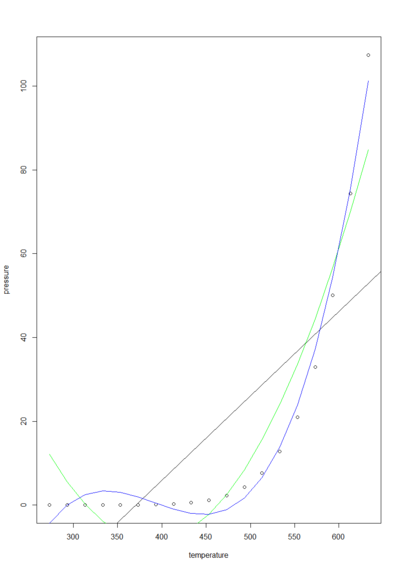
Linearity。

It is assumed that the relationship between each predictor variable and the criterion variable is linear

Violation consequences

• The predictions may systematically overestimate the actual values for one range of values on a predictor variable
• They may underestimate them for another range

Relationships between predictor variables。

• Ideally, predictor variables would be independent but it is hardly ever the case

Interaction

Two independent variables interact if the effect of one of the variables differs depending on the level of the other variable

• Adding sugar and stirring the coffee (Criterion: sweetness of the coffee)
• Adding carbon to steel and quenching (Criterion: strength of the material)
• The IQ of a person and their knowledge/education (Criterion: solving a specific problem)
• Advertising spending and advertisement design (Criterion: revenue from sales)

Quiz。

Please find the quiz here

Quiz

1 The multiple correlation (R) is: (check all that apply)

	A:The correlation between predicted and observed scores
	B:The sum of the simple r's
	C:The highest simple r
	D:Always between 0 and 1 (inclusive)

Answer >>

A,D

R is the correlation between predicted and observed scores when there are two or more predictors. It is always between 0 and 1.

2 In multiple regression there are:

	Multiple criterion variables
	Multiple predictor variables
	Only two predictor variables

Answer >>

Multiple predictor variables.

Having two or more predictor variables is what distinguishes multiple regression from simple regression.

3 In the regression equation Y' = b₁X₁ + b₂X₂ + A, if b₁ = 5, then how much would the predicted value of Y differ for two observations that had the same value of X₂ but differed by 7 on X₁?

Answer >>

35

A change of 1 on b1 is associated with a change of 5 on Y' so a difference of 7 would be associated with a predicted difference of 5 x 7, which is 35.

4 Which of the following assumptions pertain to inferential statistics in multiple regression?

	A:The predictor variables are normally distributed
	B:The criterion variable is normally distributed
	C:The errors of prediction (the residuals) are normally distributed
	D:The variance about the regression line is the same for all predicted values
	E:The predictor variables are linearly related to the criterion

Answer >>

C, D, E