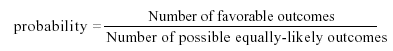Statistics for Decision Makers - 05.02 - Probability - Basic Concepts
Probability of a Single Event。
- If you roll a six-sided die, there are six possible outcomes, and each of these outcomes is equally likely.
- A six is as likely to come up as a three, and likewise for the other four sides of the die
- The probability that a one will come up is 1/6
- What is the probability that either a one or a six will come up?
- The two outcomes about which we are concerned (a one or a six coming up) are called favourable outcomes
- Given that all outcomes are equally likely, we can compute the probability of a one or a six using the formula:
- In this case there are two favourable outcomes and six possible outcomes:
P(1 or 6) = 2/6 = 1/3
Favourable Outcomes。
- Don't be misled by our use of the term "favourable"
- It can be use to work out probability of having cancer.
- Favourable in this case would be to have cancer
- You should understand it in the sense of "favourable to the event in question happening"
Example 1。
What is the probability that a card drawn at random from a deck of playing cards will be an ace?
- Favourable outcomes
- The deck has 4 aces, there are 4 favourable outcomes.
- Possible outcomes
- Since the deck has 52 cards, there are 52 possible outcomes.
The probability is therefore 4/52 = 1/13.
- What about the probability that the card will be a club?
- Since there are 13 clubs, the probability is 13/52 = 1/4.
Example 2。
- There are 20 fruits in a bag: 14 apples and 6 plums
- If you pick a fruit at random, what is the probability that it will be an apple?
- There are 20 possible fruits that could be picked, so the number of possible outcomes is 20
- Of these 20 possible outcomes, 14 are favourable (apples), so the probability that the fruit will be an apple is 14/20 = 7/10
- Is that correct?
Problem Description。
- It must be assumed that the probability of picking any of the fruit is the same as the probability of picking any other
- This wouldn't be true if (let us imagine) the plums are smaller than the apples
- The apples would come to hand more readily when you sampled from the bag
- Let us keep in mind, therefore, that when we assess probabilities in terms of the ratio of favourable cases to all potential cases, we rely heavily on the assumption of equal probability for all outcomes
Example 3。
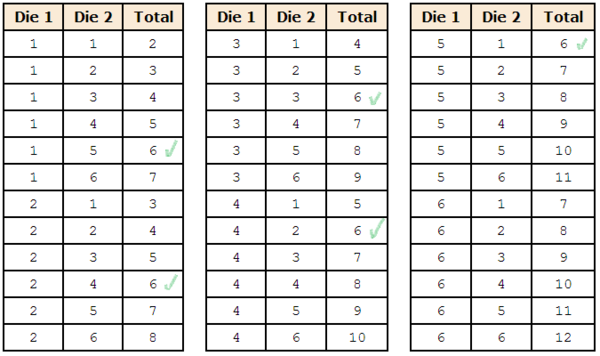
- You throw 2 dice. What is the probability that the sum of the two dice will be 6?
- There are 36 possible outcomes since each die can come up one of six ways
- You can see that 5 of the 36 possibilities total 6
- Therefore, the probability is 5/36
Opposite (Complement) Event。
If you know the probability of an event occurring, it is easy to compute the probability of the event not occurring
- If P(A) is the probability of Event A, then 1 - P(A) is the probability that the event does not occur
- The probability that the total is 6 is 5/36
- Therefore, the probability that the total is not 6 is 1 - 5/36 = 31/36
Probability of Two (or more) Independent Events。
Events A and B are independent events if the probability of Event B occurring is the same whether or not Event A occurs.
Example 1
A fair coin is tossed two times.
- The probability that a head comes up on the second toss is 1/2 regardless of whether or not a head came up on the first toss
- The two events are (1) first toss is a head and (2) second toss is a head
- So these events are independent
Example 2
Consider the two events
- "It will rain tomorrow in Houston"
- "It will rain tomorrow in Galveston" (a city near Houston)
These events are not independent because it is more likely that it will rain in Galveston on days it rains in Houston than on days it does not
Probability of A and B。
- When two events are independent, the probability of both occurring is the product of the probabilities of the individual events
- More formally, if events A and B are independent, then the probability of both A and B occurring is:
P(A and B) = P(A) x P(B) where P(A and B) is the probability of events A and B both occurring
Example 1。
If you flip a coin twice, what is the probability that it will come up heads both times?
- Event A is that the coin comes up heads on the first flip
- Event B is that the coin comes up heads on the second flip
Since both P(A) and P(B) equal 1/2, the probability that both events occur is 1/2 x 1/2 = 1/4.
Example 2。
If you flip a coin and roll a six-sided die, what is the probability that the coin comes up heads and the die comes up 1?
- Since the two events are independent, the probability is simply the probability of a head (which is 1/2) times the probability of the die coming up 1 (which is 1/6)
- Therefore, the probability of both events occurring is 1/2 x 1/6 = 1/12
Example 3。
- You draw a card from a deck of cards, put it back, and then draw another card
- What is the probability that the first card is a heart and the second card is black?
- Since there are 52 cards in a deck and 13 of them are hearts, the probability that the first card is a heart is 13/52 = 1/4
- Since there are 26 black cards in the deck, the probability that the second card is black is 26/52 = 1/2
- The probability of both events occurring is therefore 1/4 x 1/2 = 1/8
Probability of A or B。
If Events A and B are independent, the probability that either Event A or Event B occurs is:
P(A or B) = P(A) + P(B) - P(A and B)
In this discussion, when we say "A or B occurs" we include three possibilities:
- A occurs and B does not occur
- B occurs and A does not occur
- Both A and B occur
- This use of the word "or" is technically called "inclusive or" because it includes the case in which both A and B occur.
- If we included only the first two cases, then we would be using an exclusive or
Example 1。
If you flip a coin two times, what is the probability that you will get a head on the first flip or a head on the second flip (or both)?
- Letting Event A be a head on the first flip and Event B be a head on the second flip, then P(A) = 1/2, P(B) = 1/2, and P(A and B) = 1/4
- Therefore,
P(A or B) = 1/2 + 1/2 - 1/4 = 3/4
Complementary Probability。
If you throw a die three times, what is the probability that one or more of your throws will come up with a 1?
- That is, what is the probability of getting a 1 on the first throw OR a 1 on the second throw OR a 1 on the third throw?
- The easiest way to approach this problem is to compute the probability of
NOT getting a 1 on the first throw AND not getting a 1 on the second throw AND not getting a 1 on the third throw
The answer will be 1 minus this probability.
- The probability of not getting a 1 on any of the three throws is 5/6 x 5/6 x 5/6 = 125/216
- Therefore, the probability of getting a 1 on at least one of the throws is 1 - 125/216 = 91/216
Conditional Probabilities。
It is often necessary to compute the probability of an event given that another event has occurred.
Example 1。
What is the probability that two cards drawn at random from a deck of playing cards will both be aces?
- Is 4/52 x 4/52 = 1/169 correct?
- The two events are not independent
- If the first card drawn is an ace, then the probability that the second card is also an ace would be lower because there would only be three aces left in the deck
- Once the first card chosen is an ace, the probability that the second card chosen is also an ace is called the conditional probability of drawing an ace
- In this case, the "condition" is that the first card is an ace
- Symbolically, we write this as:
P(ace on second draw | an ace on the first draw)
- The vertical bar "|" is read as "given," so the above expression is short for: "The probability that an ace is drawn on the second draw given that an ace was drawn on the first draw"
- What is this probability?
- Since after an ace is drawn on the first draw, there are 3 aces out of 51 total cards left
- This means that the probability that one of these aces will be drawn is 3/51 = 1/17
- If Events A and B are not independent, then P(A and B) = P(A) x P(B|A)
- The probability of drawing two aces from a deck is 4/52 x 3/51 = 1/221.
Question。
- A fair coin is flipped five times and comes up heads each time
- What is the probability that it will come up heads on the sixth flip?
Gambler's Fallacy。
- The correct answer is, of course, 1/2
- But many people believe that a tail is more likely to occur after throwing five heads
- Their faulty reasoning may go something like this: "In the long run, the number of heads and tails will be the same, so the tails have some catching up to do"
Quiz。
Quiz
<quiz display=simple>
{Select all that apply. Which of the following pairs are independent events?
|type="[]"} +Two coin flips -A student's midterm and final grades in a class -Draw an ace, leave it out, then draw an ace again +Draw an ace, put it back, then draw an ace again
{
Answer >>
Two coin flips; draw an ace, put it back, then draw an ace again
Two events are independent if the occurrence of one has no effect on the probability of the occurrence of the other. A student's test grades are not independent because a student who does well on the midterm understands the material and is therefore more likely to do well on the final. Two draws of an ace without replacement are not independent because what you get on your first draw affects the probability of getting an ace on the second draw. This is a conditional probability.
}
{Which of the following pairs may be considered independent events by a manager? |type="()"} -The trains are delayed and the road is blocked -You lose money invested in gold and you lose money invested in property -A solar storm and flooding -Your laptop breaks down and your desktop computer breaks down +You win the lottery and stock prices go up {
Answer >>
In reality almost every event is somehow related.
If the train is delayed, it might be due to bed weather, therefore it increases the chances of a traffic jam.
Commodity markets do rely on property prices as an alternative form of investment.
Solar storm can trigger weather anomalies.
A power surge can cause both machines to break down.
Usually chances of winning the lottery do not depend on stock market prices, though some may argue that if someone will invest the prize in stocks than the events are not truly independent.
} {You win a game if you roll a die and get an odd number and flip a coin and get tails. What is the probability that you win?
|type="{}"} { 0.25 | 3/12 | 1/4 }
{
Answer >>
0.25
P(Odd # AND Tails) equals 3/6 x 1/2 equals .5 x .5 equals 0.25
}
{You win $1 every time you flip a coin and get heads. You win $3 every time you roll a die and get a 5. You roll the die and flip the coin one time each. What is the probability that you win money from at least one game?
|type="{}"}
{ 0.58 | 7/12 }
{
Answer >>
0.58
The probability that you win $1 OR $3 (or both games) is: (1/2) + (1/6) - (1/2)(1/6) equals 7/12 equals 0.58
}
{A survey showed that 60% of all adults in your city take public transport to work. If 3 people are chosen at random, what is the probability that they will all take public transport to work?
|type="{}"}
{ 0.216 }
{
Answer >>
0.216
The probability that person 1 AND person 2 AND person 3 will take public transportation is: .6 x .6 x.6 equals 0.216
}
{You win a game if you roll a 3 on at least one of your two dice. What is the probability that you win?
|type="{}"} { 0.31 | 11/36 }
{
Answer >>
0.31
The probability of getting a 3 on the first roll OR a 3 on the second roll is: (1/6) + (1/6) - (1/6)(1/6) equals 11/36 equals 0.31
}
{If you throw a die four times, what is the probability that one or more of your throws will come up with a 4?
|type="{}"} { 0.52 }
{
Answer >>
0.52
The probability of NOT getting a 4 on any roll is: (5/6)(5/6)(5/6)(5/6) equals .48, so the probability of rolling at least one 4 is: 1 - .48 equals 0.52
}
{What is the probability that you draw two cards from a deck and both of them are spades?
|type="{}"} { 0.0588 }
{
Answer >>
0.0588
P (spade on the first draw) equals 13/52 equals .25
P (spade on the second draw given that spade on the first draw) equals 12/51 equals .235
.25*.235 equals 0.0588
}
{You flip a coin three times. Is it more likely to get heads all three times or heads, then tails, then heads?
|type="()"} -HHH -HTH +They are both equally likely
{
Answer >>
They are both equally likely
There are 8 possible outcomes for flipping a coin 3 times, so each has a 1/8 probability.
}
