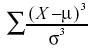Statistics for Decision Makers - 03.04 - Summarizing Distributions - Distributions
Jump to navigation
Jump to search
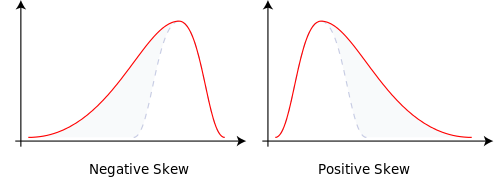
Shapes of distributions can differ in skew and/or kurtosis.
Skew。
A distribution is skewed if one tail extends out further than the other.
- A distribution has positive skew (is skewed to the right) if the tail to the right is longer
- A distribution has a negative skew (is skewed to the left) if the tail to the left is longer
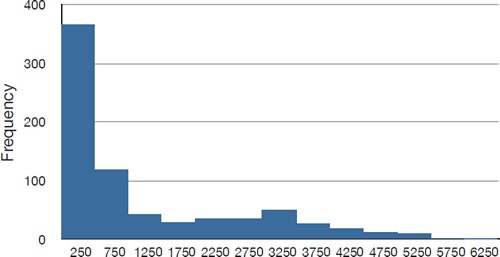
Positive Skew Example。
- The histogram above shows the salaries of major league baseball players (in thousands of dollars)
- It shows a distribution with a very large positive skew
- The mean and median of the baseball salaries are $1,183,417 and $500,000 respectively
- Thus, for this highly-skewed distribution, the mean is more than twice as high as the median
Measures of skew。
Pearson's measure of skew
- Based on the relationship between skew and the relative size of the mean and median
- It is just simple and convenient numerical index of skew
- The standard deviation of the baseball salaries is 1,390,922
- Therefore, Pearson's measure of skew for this distribution is 3(1,183,417 - 500,000)/1,390,922 = 1.47
Third moment about the mean
- Although Pearson's measure is a good one, the following measure is more commonly used
- It is sometimes referred to as the third moment about the mean
Quiz。
Quiz
