Standard Normal Distribution

Normal distributions do not necessarily have the same means and standard deviations.

Standard normal distribution

A normal distribution with a mean of 0 and a standard deviation of 1

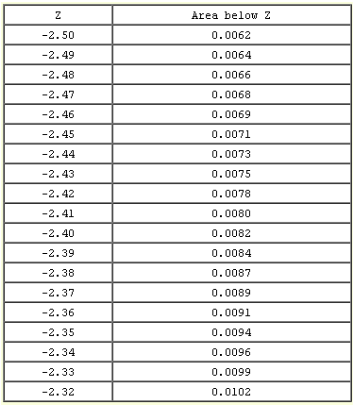
Area below Z

• The first column titled "Z" contains values of the standard normal distribution; the second column contains the area below Z.
• Since the distribution has a mean of 0 and a standard deviation of 1, the Z column is equal to the number of standard deviations below (or above) the mean.

Example

• a Z of -2.5 represents a value 2.5 standard deviations below the mean.
• The area below Z is 0.0062.

Formula

A value from any normal distribution can be transformed into its corresponding value on a standard normal distribution using the following formula:

Z = (X - μ)/σ

Where:
Z is the value on the standard normal distribution,
X is the value on the original distribution,
μ is the mean of the original distribution and
σ is the standard deviation of the original distribution.

Example

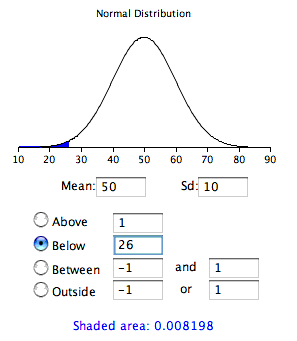
As a simple application, what portion of a normal distribution with a mean of 50 and a standard deviation of 10 is below 26? Applying the formula, we obtain

Z = (26 - 50)/10 = -2.4

• From the table above, we can see that 0.0082 of the distribution is below -2.4.
• There is no need to transform to Z if you use the applet as shown below.

Standardizing the Distribution

If all the values in a distribution are transformed to Z scores, then the distribution will have a mean of 0 and a standard distribution. This process of transforming a distribution to one with a mean of 0 and a standard deviation of 1 is called standardizing the distribution

Quiz

1 A standard normal distribution has:

	a mean of 1 and a standard deviation of 1
	a mean of 0 and a standard deviation of 1
	a mean larger than its standard deviation
	all scores within one standard deviation of the mean

Answer >>

a mean of 0 and a standard deviation of 1

The standard normal distribution is defined as a normal distribution with a mean of 0 and a standard deviation of 1.

2 A number 1.5 standard deviations below the mean has a z score of:

	1.5
	-1.5
	3
	more information is needed

Answer >>

-1.5

Z is equal to the number of standard deviations below or above the mean. Numbers below the mean have negative Z scores.

3 A distribution has a mean of 16 and a standard deviation of 6. What is the Z score that corresponds with 25?

Answer >>

1.5

25 is 1.5 SDs above the mean: Z is (X - M)/SD. (25 - 16)/6 is 1.5

4 A distribution has a mean of 18 and a standard deviation of 5. Use the table presented in this section to determine the proportion of the scores (area) below 6.

}