Multinomial Distribution
The binomial distribution allows one to compute the probability of obtaining a given number of binary outcomes.
- For example, it can be used to compute the probability of getting 6 heads out of 10 coin flips.
- The flip of a coin is a binary outcome because it has only two possible outcomes: heads and tails.
The multinomial distribution can be used to compute the probabilities in situations in which there are more than two possible outcomes.
- For example, suppose that two chess players had played numerous games and it was determined that the probability that Player A would win is 0.40, the probability that Player B would win is 0.35, and the probability that the game would end in a draw is 0.25.
The following formula gives the probability of obtaining a specific set of outcomes when there are three possible outcomes for each event:
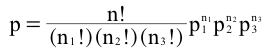p is the probability,
n is the total number of events
n1 is the number of times Outcome 1 occurs,
n2 is the number of times Outcome 2 occurs,
n3 is the number of times Outcome 3 occurs,
p1 is the probability of Outcome 1
p2 is the probability of Outcome 2, and
p3 is the probability of Outcome 3.
The formula for k outcomes is
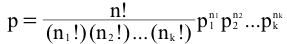
Note that the binomial distribution is a special case of the multinomial when k = 2.
Example
The multinomial distribution can be used to answer questions such as:
"If these two chess players played 12 games, what is the probability that Player A would win 7 games, Player B would win 2 games, and the remaining 3 games would be drawn?"
For this example,
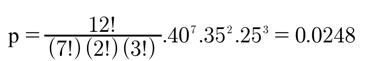n = 12 (12 games are played),
n1 = 7 (number won by Player A),
n2 = 2 (number won by Player B),
n3 = 3 (the number drawn),
p1 = 0.40 (probability Player A wins)
p2 = 0.35(probability Player B wins)
p3 = 0.25(probability of a draw)
Quiz
