Introduction to Simple Linear Regression
Simple Regression
In simple linear regression, we predict scores on one variable from the scores on a second variable.
- Criterion variable: The variable we are predicting, referred to as Y.
- Predictor variable: The variable we are basing our predictions on, referred to as X.
When there is only one predictor variable, the prediction method is called simple regression
- In simple linear regression, the predictions of Y when plotted as a function of X form a straight line.
Simple Regression Example
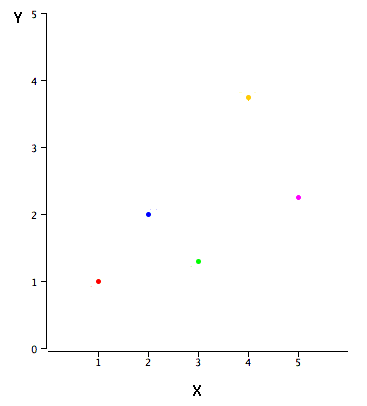
Data in the table are plotted in the graph below.
- there is a positive relationship between X and Y.
- If you were going to predict Y from X,
- the higher the value of X, the higher your prediction of Y.
|
X | Y |
|---|---|---|
| 1.00 | 1.00 | |
| 2.00 | 2.00 | |
| 3.00 | 1.30 | |
| 4.00 | 3.75 | |
| 5.00 | 2.25 |
Linear regression
- Linear regression consists of finding the best-fitting straight line through the points.
- The best-fitting line is called a regression line
- Example
Regression Line=
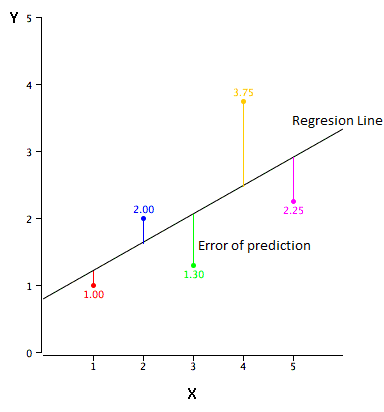
The error of prediction
The error of prediction for a point is the value of the point minus the predicted value (the value on the line)
- Example
- the predicted values (Y') and the errors of prediction (Y-Y').
- the first point has a Y of 1.00 and a predicted Y of 1.21. Therefore its error of prediction is -0.21.
| X | Y | Y' | Y-Y' | (Y-Y')2 |
|---|---|---|---|---|
| 1.00 | 1.00 | 1.210 | -0.210 | 0.044 |
| 2.00 | 2.00 | 1.635 | 0.365 | 0.133 |
| 3.00 | 1.30 | 2.060 | -0.760 | 0.578 |
| 4.00 | 3.75 | 2.485 | 1.265 | 1.600 |
| 5.00 | 2.25 | 2.910 | -0.660 | 0.436 |
Regression Line
The Best Fitting Line
- What does it meant by "best fitting line" ?
- By far the most commonly used criterion for the best fitting line is the line that minimizes the sum of the squared errors of prediction.
- That is the criterion that was used to find the line in previous regression line graph.
- The last column in the previous table shows the squared errors of prediction.
- The sum of the squared errors of prediction shown in the previous table is lower than it would be for any other regression line.
The Formula for a Regression Line
The formula for a regression line
Y' = bX + A where Y' is the predicted score, b is the slope of the line, and A is the Y intercept.
- Example
The equation for the line in the previous graph is
- Y' = 0.425X + 0.785
- For X = 1, Y' = (0.425)(1) + 0.785 = 1.21
- For X = 2, Y' = (0.425)(2) + 0.785 = 1.64
Computing the Regression Line
- In the age of computers, the regression line is typically computed with statistical software.
- However, the calculations are relatively easy are given here for anyone who is interested.
The calculations are based on the statistics below.
- MX is the mean of X
- MY is the mean of Y
- sX is the standard deviation of X
- sY is the standard deviation of Y
- r is the correlation between X and Y
| MX | MY | sX | sY | r |
|---|---|---|---|---|
| 3 | 2.06 | 1.581 | 1.072 | 0.627 |
The Slope of the Regression Line
The slope (b) can be calculated as follows:
b = r sY/sX
and the intercept (A) can be calculated as
A = MY - bMX
For these data,
b = (0.627)(1.072)/1.581 = 0.425 A = 2.06 - (0.425)(3)=0.785
- The calculations have all been shown in terms of sample statistics rather than population parameters.
- The formulas are the same; simply use the parameter values for means, standard deviations, and the correlation.
Standardized Variables
- The regression equation is simpler if variables are standardized so that their means are equal to 0 and standard deviations are equal to 1, for then b = r and A = 0.
- This makes the regression line:
ZY' = (r)(ZX) where ZY' is the predicted standard score for Y, r is the correlation, and ZX is the standardized score for X.
Note that the slope of the regression equation for standardized variables is r.
Example
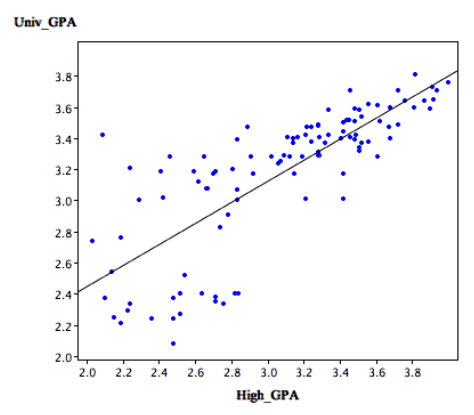
The case study, Predicting GPA contains high school and university grades for 105 computer science majors at a local state school.
- We now consider how we could predict a student's university GPA if we knew his or her high school GPA.
- The correlation is 0.78 The regression equation is
GPA' = (0.675)(High School GPA) + 1.097
- A student with a high school GPA of 3 would be predicted to have a university GPA of
GPA' = (0.675)(3) + 1.097 = 3.12
- The graph shows University GPA as a function of High School GPA
- There is a strong positive relationship between them
Assumptions
- It may surprise you, but the calculations shown in this section are assumption free.
- Of course, if the relationship between X and Y is not linear, a different shaped function could fit the data better.
- Inferential statistics in regression are based on several assumptions.
Quiz