Inferential Statistics for b and r
Jump to navigation
Jump to search
Assumptions
- Although no assumptions were needed to determine the best-fitting straight line, assumptions are made in the calculation of inferential statistics.
- Naturally, these assumptions refer to the population, not the sample.
- Linearity: The relationship between the two variables is linear.
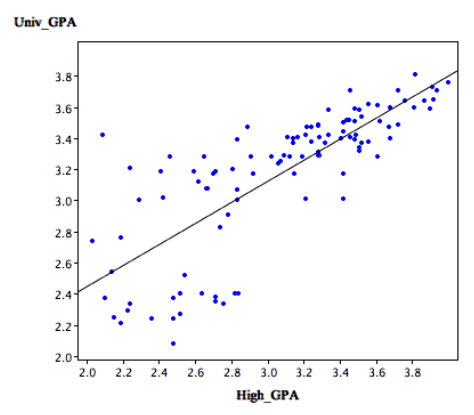
- Homoscedasticity: The variance around the regression line is the same for all values of X. A clear violation of this assumption is shown in below. (Notice that the predictions for students with high high-school GPAs are very good, whereas the predictions for students with low high-school GPAs are not very good. In other words, the points for students with high high-school GPAs are close to the regression line, whereas the points for low high-school GPA students are not.)
- The errors of prediction are distributed normally. This means that the deviations from the regression line are normally distributed. It does not mean that X or Y is normally distributed.
Significance Test for the Slope (b)
As applied here, the statistic is the sample value of the slope (b) and the hypothesized value is 0.
- The number of degrees of freedom for this test is
df = N-2 where N is the number of pairs of scores.
- The estimated standard error of b is computed using the following formula
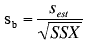 sb is the estimated standard error of b,
sest is the standard error of the estimate
SSX is the sum of squared deviations of X from the mean of X
sb is the estimated standard error of b,
sest is the standard error of the estimate
SSX is the sum of squared deviations of X from the mean of X
- SSX is calculated as
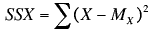 where Mx is the mean of X
where Mx is the mean of X
- The standard error of the estimate can be calculated as
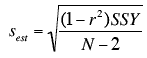
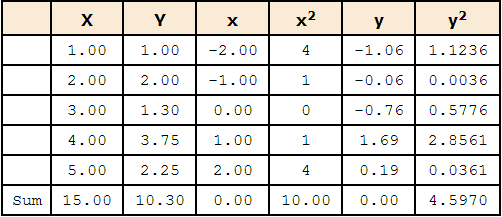
Example
- The column X has the values of the predictor variable
- The column Y has the values of the criterion variable
- The column x has the differences between the values of column X and the mean of X
- The column x2 is the square of the x column
- The column y has the differences between the values of column Y and the mean of Y.
- The column y2 is simply square of the y column
- The standard error of the estimate
The computation of the standard error of the estimate (sest) for these data is shown in the section on the standard error of the estimate. It is equal to 0.964.
sest = 0.964
- SSX
SSX is the sum of squared deviations from the mean of X. i.e. it is equal to the sum of the x2 column and is equal to 10.
SSX = 10.00
We now have all the information to compute the standard error of b:
- the slope (b) is
b= 0.425. df = N-2 = 5-2 = 3.
- The p value for a two-tailed t test is 0.26.
- Therefore, the slope is not significantly different from 0.
Confidence Interval for the Slope
- The method for computing a confidence interval for the population slope is very similar to methods for computing other confidence intervals.
- For the 95% confidence interval, the formula is:
lower limit: b - (t.95)(sb) upper limit: b + (t.95)(sb) where t.95 is the value of t to use for the 95% confidence interval
Example
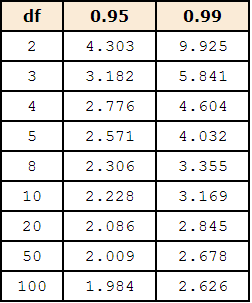
- The values of t to be used in a confidence interval can be looked up in a table of the t distribution.
- A small version of such a table is shown above.
- The first column, df, stands for degrees of freedom.
- You can also use the "inverse t distribution" calculator to find the t values to use in a confidence interval.
- Applying these formulas to the example data,
lower limit: 0.425 - (3.182)(0.305) = -0.55 upper limit: 0.425 + (3.182)(0.305) = 1.40
Significance Test for the Correlation
The formula for a significance test of Pearson's correlation is shown below:
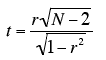 where N is the number of pairs of scores.
where N is the number of pairs of scores.
For the example data,
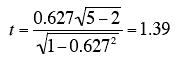
Notice that this is the same t value obtained in the t test of b. As in that test, the degrees of freedom is
N - 2 = 5 -2 = 3.
Quiz