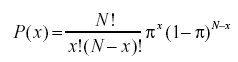History of Normal Distribution

Binomial and Normal distribution

Example

Example: To solve the problem "If a fair coin is flipped 100 times, what is the probability of getting 60 or more heads?”,

you need to use the formula more than 40 times.

• Abraham de Moivre, an 18th century statistician and consultant to gamblers was often called upon to make these lengthy computations,
• de Moivre noted that when the number of events (coin flips) increased, the shape of the binomial distribution approached a very smooth curve.

Importance of Normal Curve

The distribution of many natural phenomena are at least approximately normally distributed

• Animals and human height and weight
• Accidents (accidental deaths, etc…)
• Most of the non-systematic errors
• Fertility rate

Galileo in the 17th century noted that these errors were symmetric and that small errors occurred more frequently than large errors

• This same distribution had been discovered by Laplace in 1778 when he derived the extremely important central limit theorem
• Laplace showed that even if a distribution is not normally distributed, the means of repeated samples from the distribution would be very nearly normal, and that the larger the sample size, the closer the distribution would be to a normal distribution.

Central Limit Theorem

In probability theory, the central limit theorem (CLT) states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed (Rice 1995).

Quiz

<quiz display=simple > { Who was the 18th century statistician and consultant to gamblers that discovered the normal curve?

|type="()"} +de Moivre -Galileo -Adrian -Gauss

{

Answer >>

de Moivre

de Moivre reasoned that if he could find a mathematical expression for the smooth curve that came about when the number of binomial events (coin flips) increased, he would be able to solve problems such as finding the probability of 60 or more heads out of 100 coin flips much more easily. The curve he discovered is now called the "normal curve."

}

{Why was the normal curve an important development?

|type="[]"} - A:It has a relatively simple formula. + B:Many natural phenomena are at least approximately normally distributed. + C:Many inferential statistics can only be computed with a normal distribution.

{

Answer >>

B,C

For example, one of the first applications of the normal distribution was to the analysis of errors of measurement made in astronomical observations. Galileo in the 17th century noted that these errors were symmetric and that small errors occurred more frequently than large errors.

}

{Who is responsible for the central limit theorem?

|type="()"} -Gauss +Laplace -Newton -Adrian

{

Answer >>

Laplace

Laplace derived the central limit theorem. Adrian and Gauss developed the formula for the normal distribution.

}