Inferential Statistics for b and r

Assumptions

• Although no assumptions were needed to determine the best-fitting straight line, assumptions are made in the calculation of inferential statistics.
• Naturally, these assumptions refer to the population, not the sample.

1. Linearity: The relationship between the two variables is linear.
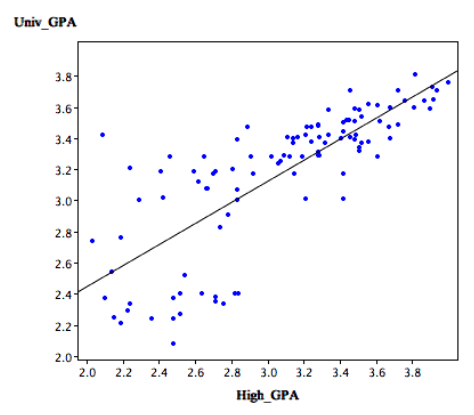
2. Homoscedasticity: The variance around the regression line is the same for all values of X. A clear violation of this assumption is shown in below. (Notice that the predictions for students with high high-school GPAs are very good, whereas the predictions for students with low high-school GPAs are not very good. In other words, the points for students with high high-school GPAs are close to the regression line, whereas the points for low high-school GPA students are not.)
3. The errors of prediction are distributed normally. This means that the deviations from the regression line are normally distributed. It does not mean that X or Y is normally distributed.

Significance Test for the Slope (b)

The general formula for a t test

As applied here, the statistic is the sample value of the slope (b) and the hypothesized value is 0.

The number of degrees of freedom for this test is

df = N-2
where N is the number of pairs of scores.

The estimated standard error of b is computed using the following formula

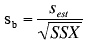sb is the estimated standard error of b, 
sest is the standard error of the estimate
SSX is the sum of squared deviations of X from the mean of X

SSX is calculated as

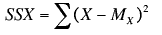where Mx is the mean of X

The standard error of the estimate can be calculated as

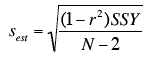
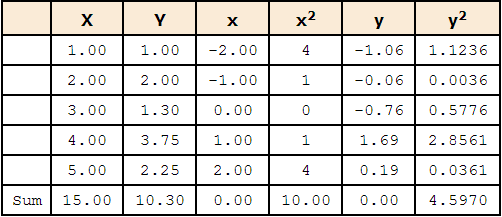
Example

• The column X has the values of the predictor variable
• The column Y has the values of the criterion variable
• The column x has the differences between the values of column X and the mean of X
• The column x² is the square of the x column
• The column y has the differences between the values of column Y and the mean of Y.
• The column y² is simply square of the y column

The standard error of the estimate

The computation of the standard error of the estimate (s_est) for these data is shown in the section on the standard error of the estimate. It is equal to 0.964.

sest = 0.964

SSX

SSX is the sum of squared deviations from the mean of X. i.e. it is equal to the sum of the x2 column and is equal to 10.

SSX = 10.00

We now have all the information to compute the standard error of b:

the slope (b) is

b= 0.425. 
df = N-2 = 5-2 = 3.

• The p value for a two-tailed t test is 0.26.
• Therefore, the slope is not significantly different from 0.

Confidence Interval for the Slope

• The method for computing a confidence interval for the population slope is very similar to methods for computing other confidence intervals.
• For the 95% confidence interval, the formula is:

lower limit: b - (t.95)(sb)
upper limit: b + (t.95)(sb)
where t.95 is the value of t to use for the 95% confidence interval

Example

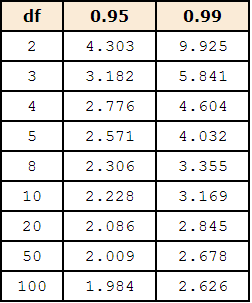
• The values of t to be used in a confidence interval can be looked up in a table of the t distribution.
• A small version of such a table is shown above.
• The first column, df, stands for degrees of freedom.
• You can also use the "inverse t distribution" calculator to find the t values to use in a confidence interval.
• Applying these formulas to the example data,

lower limit: 0.425 - (3.182)(0.305) = -0.55
upper limit: 0.425 + (3.182)(0.305) = 1.40

Significance Test for the Correlation

The formula for a significance test of Pearson's correlation is shown below:

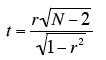where N is the number of pairs of scores. 

For the example data,

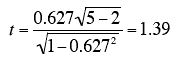
Notice that this is the same t value obtained in the t test of b. As in that test, the degrees of freedom is

N - 2 = 5 -2 = 3.

Quiz

1 Which of the following are assumptions made in the calculation of regression inferential statistics?

	A:The errors of prediction are normally distributed.
	B:X is normally distributed.
	C:Y is normally distributed.
	D:The variance around the regression line is the same for all values of X.
	E:The relationship between X and Y is linear.

Answer >>

A,D,E

The assumptions are linearity, homoscedasticity, and normally distributed errors. See the text for more information.

2 The slope of a regression line is 0.8, and the standard error of the slope is 0.3. The sample used to compute this regression line consisted of 12 participants. Compute the 95% confidence interval for the slope. Type the upper limit of the confidence interval in the box below.

Answer >>

1.47

Use the table in this section or the inverse t distribution calculator to find that the critical value is t(N-2).

t(10) s 2.23.

The upper limit of the 95% CI is b + (t)(sb)

.8 + 2.23(.3) equals to 1.47.

3 In a sample of 20, the correlation between two variables is .5. Determine if this correlation is significant at the .05 level by calculating the t value.

Answer >>

2.45

t is (r) sqrt(N-2)/sqrt(1-r2) equals to (0.5) sqrt(18)/sqrt(1-.25) is 2.45 (This is significant at the .05 level.)

4 Calculate the lower limit of the 95% confidence interval for the correlation of .75 (N = 25).

Answer >>

0.505

First, convert r to z' (so .75 -> .973). The standard error of z' is 1/sqrt(N-3)is .213.

Lower limit of CI is .973 - 1.96(.213) equals to 0.556. Now convert back from z' to r. r is .505