Statistics for Decision Makers - 05.05 - Probability - Base Rate Fallacy
Jump to navigation
Jump to search
<slideshow style="nobleprog" headingmark="。" incmark="…" scaled="false" font="Trebuchet MS" footer="www.NobleProg.co.uk" subfooter="Training Courses Worldwide">
- title
- 05.05 - Probability - Base Rate Falacy
- author
- Bernard Szlachta (NobleProg Ltd) bs@nobleprog.co.uk
</slideshow>
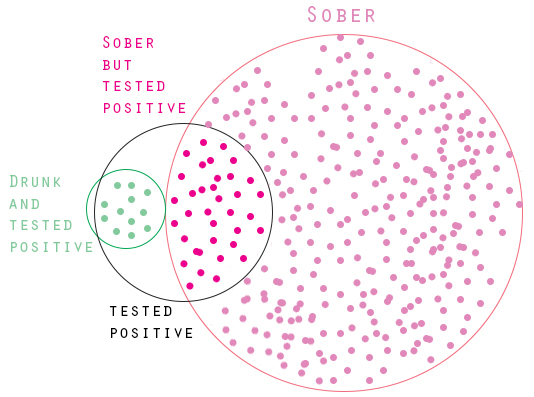
Drunk Driving。
- Breathalysers display a false result in 5% of the cases tested
- They never fail to detect a truly drunk person
- 1/1000 of drivers are driving drunk
- Policemen then stop a driver at random, and test them
- The breathalyser indicates that the driver is drunk
- How high is the probability the driver is really drunk?
| Result\Reality | Drunk | Sober |
|---|---|---|
| Test Positive | 1 | 0.05 |
| Test Negative | 0 | 0.95 |
| Historic Data | 0.001 | 0.999 |
Drunk Driving。
Let us assume we tested 1,000,000 people.
| True Condition | |||
|---|---|---|---|
| Drunk | Not Drunk | ||
| 1,000 | 999,000 | ||
| Positive | Negative | Positive | Negative |
| 1,000 | 0 | 49,950 | 949,050 |
- How many of those people tested positive?
- How many of those who tested positive were really drunk?
- What is a "favourable" outcome?
- How many "favourable" outcomes are there?
- How many possible outcomes are there?
- What is the probability of a person who is tested being really drunk?
Drunk Driving。
Let us assume we tested 1,000,000 people.
| True Condition | |||
|---|---|---|---|
| Drunk | Not Drunk | ||
| 1,000 | 999,000 | ||
| Positive | Negative | Positive | Negative |
| 1,000 | 0 | 49,950 | 949,050 |
- How many of those people tested positive?
1,000 + 49,950 = 50,950
- How many of those who tested positive were really drunk?
1000
- What is the probability of a person who is tested being really drunk?
1000/50,950=0.01962
Drunk Driving。
Base Rate Fallacy。
- The Base Rate in our case is 0.001 and 0.999 probabilities.
- An overwhelming proportion of people are sober, therefore the probability of a false positive (5%) is much more prominent than the 100% probability of a true positive.
- People tend to simply ignore the base rates, hence it is called (base rate neglect).
- In other words, no matter what the base rates, people tend to look at only the "test accuracy rate".
Base Rate Fallacy Examples。
- Detecting terrorists
- Detecting a rare disease
- Detecting prospective customers (provided that most people will not buy our product)
- Some DNA tests
Bayes theorem。
- What is the probability that a driver is drunk given that the breathalyser indicates that he/she is drunk?
Bayes' Theorem tells us that:
We were told the following in the first paragraph:
After using Bayes' Theorem:
Is a promotion really working?。
An online advertising company knows (based on its historical record) that 10% of the people who try the trial version of their services will convert into paying customers.
- You propose to introduce a promotion: each new customer will be granted a free $100 for advertising
- You know that some people will just register to use the $100 even if they do not intend to convert into paying customers
- You want to test the effectiveness of the free $100 promotion
- After running the promotion, 40% of customers who converted used the $100 promotion
- Also, 10% of prospects who did not convert used the promotion
Is the promotion really working?。
- Does the promotion increase the probability of conversion?
- Events
Prom: Customer uses the promotion NotProm: Customer does not use the promotion Con: Customer converts NotCon: Customer does not convert
- P(Con) = 0.1
- An online advertising company knows, based on its historical record, that 10% of the people who try the trial version of their services will convert into customers
- P(Prom|Con) = 0.4
- After running the promotion, 40% of customers who converted used the $100 promotion
- P(Prom|NotCon) = 0.1
- Also, 10% of prospects who used the promotion did not convert
- Compute complementary probabilities
P(NotCon) = 0.9 P(NotProm|Con) = 0.6 P(NotProm|NotCon) = 0.9
- Does the promotion increase probability of conversion?
P(Con|Prom) > P(Con) = 0.1 P(Con|Prom) from BaysTheorm = 0.308
Quiz。
Quiz