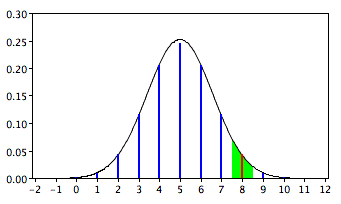
Normal Approximation to the Binomial

• Normal distribution can be used to approximate the binomial distribution.
• What is probability that you would get 8 heads out of 10 flips?

The binomial distribution:

μ = Nπ = (10)(0.5) = 5
σ2 = Nπ(1-π)= (10)(0.5)(0.5) = 2
σ = 1.5811

• Lets round off and consider any value from 7.5 to 8.5 to represent an outcome of 8 head
• We calculate the area under normal curve from 7.5 to 8.5 obtaining 8 heads.

First we compute the area below 8.5, then subtract the area below 7.5.

The results of using the normal area calculator to find the area below 8.5 and 7.5 are shown below.

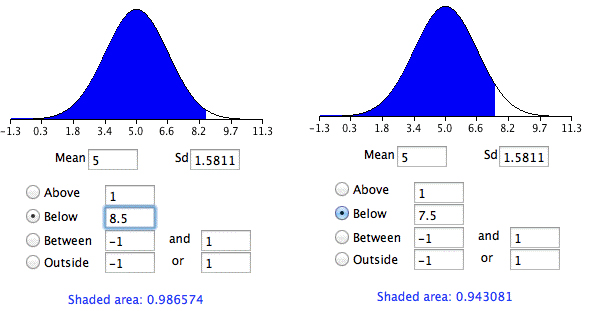
• The differences between the areas is 0.044 which is the approximation of the binomial probability.
• For these parameters, the approximation is very accurate.
• The accuracy of the approximation depends on the values of N and π
• A rule of thumb is that the approximation is good if both Nπ and N(1-π) are both greater than 10.

Quiz

1 Suppose you have a normal distribution with a mean of 6 and a standard deviation of 1. What is the probability of getting a Z score of exactly 1.2?

	0.0
	0.1
	0.01
	0.001

Answer >>

0

Because the normal distribution is continuous, the probability of any one specific point is 0.

2 You decide to use the normal distribution to approximate the binomial distribution. You want to know the probability of getting exactly 6 tails out of 10 flips. First you find the mean and SD of the normal distribution, and then you compute the area:

	at exactly 6
	from 5.5 to 6.5
	from 0 to 6
	from 6 to 10

Answer >>

from 5.5 to 6.5

Because the normal distribution is continuous, the probability of any one specific point is 0. The solution is to round off and consider any value from 5.5 to 6.5 to represent an outcome of 6 tails. Using this approach, we figure out the area under a normal curve from 5.5 to 6.5.

3 You decide to use the normal distribution to approximate the binomial distribution. You want to know the probability of getting from 7 to 13 heads out of 20 flips. You compute the area:

	from 7.5 to 13.5
	from 7.5 to 12.5
	from 7 to 13
	from 6.5 to 13
	from 6.5 to 13.5

Answer >>

from 6.5 to 13.5

In order to include 7 flips, you need to start a little below it (6.5), and to include 13 flips, you need to go a little past it (13.5). So, you calculate the area from 6.5 to 13.5.

4 The normal approximation to the binomial is most accurate for which of the following probabilities?

	0.2
	0.5
	0.8

Answer >>

{{{1}}}

5 The normal approximation to the binomial is most accurate for which of the following sample sizes?

	4
	8
	12

Answer >>

12

The binomial distribution approaches a normal distribution as the sample size increases. Therefore the approximation is best when the sample size is highest.