Chi Square Distribution
Prerequisites
- Distributions, Standard Normal Distribution, Degrees of Freedom
Define the Chi Square distribution in terms of squared normal deviates
- The Chi Square Distribution is the distribution of the sum of squared standard normal deviates
- The degrees of freedom of the distribution is equal to the number of standard normal deviates being summed
- Therefore, Chi Square with one degree of freedom, written as χ2(1), is simply the distribution of a single normal deviate squared
- The area of a Chi Square distribution below 4 is the same as the area of a standard normal distribution below 2 since 4 is 22.
Example
- You sample two scores from a standard normal distribution, square each score, and sum the squares.
- What is the probability that the sum of these two squares will be six or higher?
- Since two scores are sampled, the answer can be found using the Chi Square distribution with two degrees of freedom
- A Chi Square calculator can be used to find that the probability of a Chi Square (with 2 df) of being six or higher is 0.05
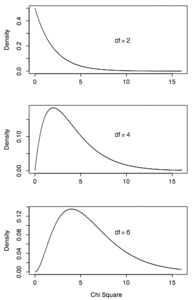
How does the shape of the Chi Square distribution change its degrees of freedom increase?
- The mean of a Chi Square distribution is its degrees of freedom.
- Chi Square distributions are positively skewed, with the degree of skew decreasing with increasing degrees of freedom
- As the degrees of freedom increase, the Chi Square Distribution approaches a normal distribution
- Notice how the skew decreases as the degrees of freedom increases.
Where can we use Chi Square distribution ?
- The Chi Square distribution is very important because many test statistics are approximately distributed as Chi Square
- Two of the more commonly tests using the Chi Square distribution are:
- tests of deviations of differences between theoretically expected and observed frequencies (one-way tables)
- the relationship between categorical variables (contingency tables)
- Numerous other tests beyond the scope of this work are based on the Chi Square distribution.
Questions