Specific Comparisons (Correlated Observations)

Learning Objectives

1. Determine whether to use the formula for correlated comparisons or independent-groups comparisons
2. Compute t for a comparison for repeated-measures data

Specific Comparisons (Correlated Observations)

• In the Weapons and Aggression case study, subjects were asked to read words presented on a computer screen as quickly as they could
• Some of the words were aggressive words such as injure or shatter
• Others were control words such as relocate or consider
• These two types of words were preceded by words that were either the names of weapons such as shot gun and grenade or non-weapon words such as rabbit or fish
• For each subject, the mean reading time across words was computed for these four conditions
• The four conditions are labeled as shown in Table 1. Table 2 shows the data for five subjects.

Description of Conditions

Variable	Description
aw	The time in milliseconds (msec) to name aggressive word following a weapon word prime.
an	The time in milliseconds (msec) to name aggressive word following a non-weapon word prime.
cw	The time in milliseconds (msec) to name a control word following a weapon word prime.
cn	The time in milliseconds (msec) to name a control word following a non-weapon word prime.

Data from Five Subjects

Subject	aw	an	cw	cn
1	447	440	432	452
2	427	437	469	451
3	417	418	445	434
4	348	371	353	344
5	471	443	462	463

One question was whether reading times would be shorter when the preceding word was a weapon word (aw and cw conditions) than when it was a non-weapon word (an and cn conditions). In other words, is

L1 = (an + cn) - (aw + cw)

greater than 0?

This is tested for significance by computing L1 for each subject and then testing whether the mean value of L1 is significantly different from 0.

Table 3 shows L1 for the first five subjects. L1 for Subject 1 was computed by

L1 = (440 + 452) - (447 + 432) = 892 - 885 = 13

L1 for Five Subjects

Subject	aw	an	cw	cn	L1
1	447	440	432	452	13
2	427	437	469	451	-8
3	417	418	445	434	-10
4	348	371	353	344	14
5	471	443	462	463	-27

• Once L1 is computed for each subject, the significance test described in the section Testing a Single Mean can be used
• First we compute the mean and the standard error of the mean for L1
• There were 32 subjects in the experiment
• Computing L1 for the 32 subjects, we find that the mean and standard error of the mean are 5.875 and 4.2646 respectively.

We then compute:

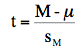M is the sample mean
μ is the hypothesized value of the population mean (0 in this case)
and sM is the estimated standard error of the mean

• The calculations show that t = 1.378
• Since there were 32 subjects, the degrees of freedom is 32 - 1 = 31
• The t distribution calculator shows that the two-tailed probability is 0.1782

Priming Effect

• A more interesting question is whether the priming effect (the difference between words preceded with a non-weapon word and words preceded by a weapon word) is different for aggressive words than it is for non-aggressive words
• That is, do weapon words prime aggressive words more than they prime non-aggressive words?
• The priming of aggressive words is (an - aw)
• The priming of non-aggressive words is (cn - cw)
• The comparison is the difference:

L2 = (an - aw) - (cn - cw)

Table 4 shows L2 for five of the 32 subjects.

L2 for Five Subjects

Subject	aw	an	cw	cn	L2
1	447	440	432	452	-27
2	427	437	469	451	28
3	417	418	445	434	12
4	348	371	353	344	32
5	471	443	462	463	-29

• The mean and standard error of the mean for all 32 subjects are 8.4375 and 3.9128 respectively
• Therefore, t = 2.156 and p = 0.039.

Multiple Comparisons

Issues associated with doing multiple comparisons are the same for related observations as they are for multiple comparisons among independent groups.

Orthogonal Comparisons

• The most straightforward way to assess the degree of dependence between two comparisons is to correlate them directly
• For the weapons and aggression data, the comparisons L1 and L2 are correlated 0.24
• Of course, this is a sample correlation and only estimates what the correlation would be if L1 and L2 were correlated in the whole population
• Although mathematically possible, orthogonal comparisons with correlated observations are very rare.

Questions

1 Here you see taste ratings for 4 cola types: Cola A (A), generic Cola A (GA), Cola B (B), and generic Cola B (GB). L1 is the difference in taste scores between non-generic and generic Colas (nongeneric - generic). What is L1 for the fourth subject?

A	GA	B	GB
  9	  6	  8	  5
 10	  6	  9	  7
 10	  5	  8	  7
  8	  4	  7	  5
 10	  5	  8	  5
  9	  7	  7	  6

Answer >>

(A+B) - (GA + GB) specifically compares generic and nongeneric cola. It is (8 + 7) - (4 + 5).

2 Calculate the standard error for L1 (L1 = A + B - GA - GB). Keep in mind this is a repeated-measures design.

A	GA	B	GB
  9	  6	  8	  5
 10	  6	  9	  7
 10	  5	  8	  7
  8	  4	  7	  5
 10	  5	  8	  5
  9	  7	  7	  6

Answer >>

Compute L1 for each subject: (6, 6, 6, 6, 8, 3) and then compute the standard deviation (1.602) which you then divide by the square root of n (n = 6) to get 0.654.

3 Calculate t for L1 (L1 = A + B - GA - GB)

A	GA	B	GB
  9	  6	  8	  5
 10	  6	  9	  7
 10	  5	  8	  7
  8	  4	  7	  5
 10	  5	  8	  5
  9	  7	  7	  6

Answer >>

Compute L1 for each subject: (6, 6, 6, 6, 8, 3) and then compute the mean (5.833) and standard deviation (1.602) which you then divide by the square root of n (n = 6) to get 0.654 Then divide the mean by the standard error of 0.654 to get 8.919.