All Pairwise Comparisons Among Means
Learning Objectives
- Define pairwise comparison
- Describe the problem with doing t tests among all pairs of means
- Calculate the Tukey hsd test
- Explain why Tukey test should not necessarily be considered a follow-up test
All Pairwise Comparisons Among Means
- Many experiments are designed to compare more than two conditions
- In the Smiles and Leniency case study, the effect of different types of smiles on the leniency showed to a person was investigated
- We can do a t test of the difference between each group mean and each other group mean
- This procedure would lead to the six comparisons shown below:
The t test and Type I Error
- The problem with this approach is that if you did this analysis, you would have six chances to make a Type I error.
- Therefore, if you were using the 0.05 significance level, the probability that you would make a Type I error on at least one of these comparisons is greater than 0.05
- The more means that are compared, the more the Type I error rate is inflated
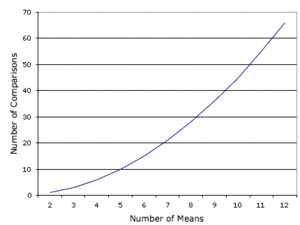
- Figure below shows the number of possible comparisons between pairs of means (pairwise comparisons) as a function of the number of means
- If there are only two means, then only one comparison can be made
- If there are 12 means, then there are 66 possible comparisons.
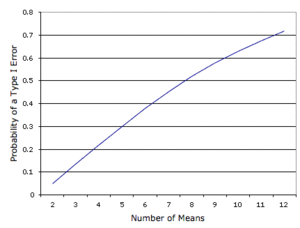
- Figure below shows probability of a Type I error as a function of the number of means
- As you can see, if you have an experiment with 12 means, the probability is about 0.70 that at least one of the 66 comparisons among means would be significant - even though all 12 population means are the same
Tukey Honestly Significant Difference (HSD) test
- The Type I error rate can be controlled using a test called the Tukey Honestly Significant Difference test or Tukey HSD for short
- The Tukey HSD is based on a variation of the t distribution that takes into account the number of means being compared
- This distribution is called the studentized range distribution.
Tukey HSD test steps
Computations are very similar to those of an independent-groups t test. The steps are outlined below:
1. Compute the means and variances of each group
| Condition | Mean | Variance |
|---|---|---|
| False | 5.37 | 3.34 |
| Felt | 4.91 | 2.83 |
| Miserable | 4.91 | 2.11 |
| Neutral | 4.12 | 2.32 |
2. Compute MSE which is simply the mean of the variances
- It is equal to 2.65.
3. Compute Q
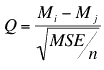
- Compute Q for each pair of means where:
- Mi is one mean
- Mj is the other mean
- n is the number of scores in each group
- For these data, there are 34 observations per group.
- The value in the denominator is 0.279.
4. Compute p for each comparison using the Studentized Range Calculator
- The degrees of freedom is equal to the total number of observations minus the number of means.
- For this experiment df = 136 - 4 = 132.
Tukey HSD test results
The tests for these data are shown below:
| Comparison | Mi-Mj | Q | p |
|---|---|---|---|
| False-Felt | 0.46 | 1.65 | 0.649 |
| False-Miserable | 0.46 | 1.65 | 0.649 |
| False-Neutral | 1.25 | 4.48 | 0.010 |
| Felt-Miserable | 0.00 | 0.00 | 1.000 |
| Felt-Neutral | 0.79 | 2.83 | 0.193 |
| Miserable-Neutral | 0.79 | 2.83 | 0.193 |
The only significant comparison is between the false smile and the neutral smile.
How to interpret non-significant results?
It is not unusual to obtain results that on the surface appear paradoxical For example, these results appear to indicate that:
- the false smile is the same as the miserable smile
- the miserable smile is the same as the neutral control
- the false smile is different from the neutral control
- This apparent contradiction is avoided if you are careful not to accept the null hypothesis when you fail to reject it
- The finding that the false smile is not significantly different from the miserable smile does not mean that they are really the same
- Rather it means that there is not convincing evidence that they are different
- Similarly, the non-significant difference between the miserable smile and the control does not mean that they are the same
- The proper conclusion is that the false smile is higher than the control and that the miserable smile is either (a) equal to the false smile, (b) equal to the control, or (c) somewhere in between.
Tukey HSD test Assumptions
Essentially the same assumptions as for an independent-groups t test:
- normality, homogeneity of variance
- independent observations
- The test is quite robust to violations of normality
- Violating homogeneity of variance can be more problematical than in the two-sample case since the MSE is based on data from all groups
- The assumption of independence of observations is important and should not be violated.
Computations for Unequal Sample Sizes (optional)
The calculation of MSE for unequal sample sizes is similar to its calculation in independent-groups t test. Here are the steps:
- Compute a Sum of Squares Error (SSE) using the following formula
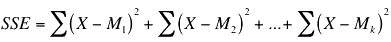
where Mi is the mean of the ith group and is the number of means.
- Compute the degrees of freedom error (dfe) by subtracting the number of groups (k) from the total number of observations (N). Therefore:
dfe N - k.
- Compute MSE by dividing SSE by dfe:
MSE = SSE/dfe.
- For each comparison of means, use the harmonic mean of the n's for the two means (nh).
All other aspects of the calculations are the same as when you have equal sample sizes.
Questions