Testing a Single Mean

Prerequisites

• Logic of Hypothesis Testing, Areas Under Normal Distributions, Sampling Distribution of the Mean, Introduction to Sampling Distributions, t Distribution

Questions

• How to test the null hypothesis that the population mean is equal to some hypothesized value?
• How to compute:
  • the probability of a sample mean being at least as high as a specified value when σ is known
  • a two-tailed probability
  • the probability of a sample mean being at least as high as a specified value when σ is estimated
• What are the assumptions required for item 3 above.

Subliminal Message Example

• An experimenter wanted to know if people are influenced by a subliminal message
• Each of 9 subjects is presented with a series of 100 pairs of pictures
• As a pair of pictures is presented, a subliminal message is presented suggesting the picture that the subject should choose
• Is the (population) mean number of times the suggested picture is chosen is equal to 50?
• H0: μ = 50
• The sample mean differed from the hypothesized population mean by 1

Subject	Frequency
1	45
2	48
3	49
4	51
5	51
6	52
7	53
8	55
9	57
Mean	M = 51

Significance Test (with known σ)

• The significance test consists of computing the probability of a sample mean differing from μ by one or more
• The sampling distribution of the mean is:
  • μ_M = μ = 50
  • :$\sigma _{\bar {x}}={\frac {\sigma }{\sqrt {n}}}$

• We assume that the standard deviation of the population is σ = 5 (only for simplification reasons, later we will cover σ estimation in details)
• μ_M = 5/3 = 1.667 = standard error of the mean

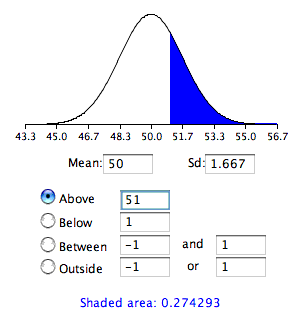
• We wish to know the probability of obtaining a sample mean of 51 or more when the sampling distribution is ${\mathcal {N}}(\mu ,\,\sigma ^{2})$ = N(50,1.667)

• The probability of the obtaining a sample mean of 51 or larger is 0.274
• Since a mean of 51 or higher is not unlikely under the assumption that the subliminal message has no effect, the effect is not significant and the null hypothesis is not rejected

Two-tailed test

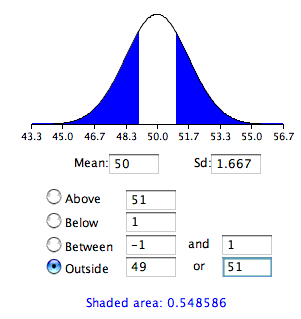
• The one-tailed test computed the probability of a sample mean being one or more points higher than the hypothesized mean of 50 and the area computed was the area above 51.
• The two-tailed test would compute the probability of a sample mean differing by one or more in either direction from the hypothesized mean of 50

• The probability is 0.54 which, as expected, is twice the probability of 0.27.
• The hypothesis that subliminal message have any effect on the viewer of the picture cannot be rejected as well.

Significance Test (with σ estimated)

• It is very rare that you would know σ and wish to estimate μ
• Typically σ is not known and is estimated in a sample by s and σ_M is estimated by s_M

ADHD Example

• For our example, we will consider the data in the ADHD treatment case study
• These data consist of the scores of 24 children with ADHD on a delay of gratification (DOG) task
• Each child was tested under four dosage levels
• Table 2 shows the data for the placebo (0mg) and highest dosage level (0.6mg) of methylphenidate
• The "Diff" column shows the difference in performance between the 0.6mg (D60) and the 0mg (D0) conditions
• These scores are positive for children who performed better in the 0.6 mg condition than in the control condition and negative for those who scored better in the control condition
• If methylphenidate has a positive effect, then the mean difference score in the population will be positive
• The null hypothesis is that the mean difference score in the population is 0 (μ=0)

D0	D60	Diff
57	62	5
27	49	22
32	30	-2
31	34	3
34	38	4
38	36	-2
71	77	6
33	51	18
34	45	11
53	42	-11
36	43	7
42	57	15
26	36	10
52	58	6
36	35	-1
55	60	5
36	33	-3
42	49	7
36	33	-3
54	59	5
34	35	1
29	37	8
33	45	12
33	29	-4

The t-test

• To test this null hypothesis, we compute t using a special case of the following formula:
  • t = (statistic - hypothesized value)/estimated standard error of the statistic

The special case for the single mean is:

• t = (M - μ) / s_M

where:

• t - the value of t we compute for the significance test
• M - the sample mean
• μ - the hypothesized value of the population mean
• s_M - the estimated standard error of the mean

• The population of difference scores is assumed to be normally distributed

• The mean (M) of the N = 24 difference scores is 4.9583
• The hypothesized value of μ is 0
• The standard deviation (s) is 7.5382

The estimate of the standard error of the mean is computed as:

• s_M = s/sqrt(N) = 7.5382/sqrt(24) = 1.54

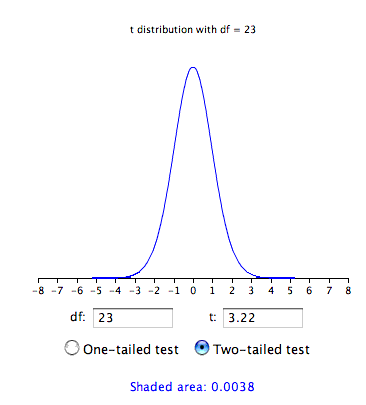
• t = 4.96/1.54 = 3.22
• df = N - 1 = 23
• P(t) for t less than -3.22 or greater than 3.22 is 0.0038
• Therefore, if the drug had no effect, the probability of finding a difference between means as large or larger (in either direction) as the difference found is very low
• Therefore the null hypothesis that the population mean difference score is zero can be rejected
• The conclusion is that the population mean for the drug condition is higher than the population mean for the placebo condition.

Review of Assumptions

• Each value is sampled independently from each other value
• The values are sampled from a normal distribution

Questions

1 You should do the test with Z rather than t when:

	The numbers are sampled from a normal distribution.
	The sample size is large.
	The sample standard deviation is known.
	The population standard deviation is known.

Answer >>

No explanation available.

2 Assume you know the standard deviation of test scores is 10 and that the distribution is normal. You sample 16 scores and find that the sample mean is 25. Find the p value for a two-tailed test of the hypothesis that the population mean is 20.

Answer >>

The standard error of the mean is 2.5. You then find the probability of a sample mean more than 25 - 20 equals 5 from the population mean of 20. This is the probability outside 15 and 25 given a distribution with a mean of 20 and a standard deviation of 2.5. The probability is 0.0455.

3 What is the standard deviation of these sample data?

Y
 -2
  1
  3
  2
 -1
  0
  4
  6

Answer >>

2.6693 Make sure you divide by N-1.

4 What is the estimated standard error of the mean based on these sample data? These are the same data as the previous question.

Y
 -2
  1
  3
  2
 -1
  0
  4
  6

Answer >>

0.94372 You divide s by the square root of N.

5 What is the value of t testing the null hypothesis that the population mean is 0? These are the same data as the previous question.

Y
 -2
  1
  3
  2
 -1
  0
  4
  6

Answer >>

You divide M = 1.625 by the standard error of the mean 0.9437 to get 1.72.

6 What is the value of two-tailed probability value testing the null hypothesis that the population mean is 0? These are the same data as the previously question.

Y
 -2
  1
  3
  2
 -1
  0
  4
  6

Answer >>

You use N-1 = 7 degrees of freedom. p = 0.1288.

7 Using these data given, what is the t statistic for a single-sample t test (null hypothesis is that μ = 0).

  Y
 -2.78
  1.74
 -0.09
  0.69
  0.34
  0.46
  1.13
  0.12

Answer >>

t &#61 0.4254

8 Using these data given, what is the t statistic for a single-sample t test (null hypothesis is that μ = 0.5).

  Y
  0.62
  0.66
  1.07
 -1.15
 -0.87
 -0.34
 -0.05
  0.63

Answer >>

t &#61 -1.509

9 Using these data given, what is the two-tailed p value for a single-sample t test (null hypothesis is that μ = 0.5).

  Y
  1.02
 -0.66
  0.83
  1.89
  1.73
  1.30
  0.95
  0.55

Answer >>

p &#61 0.1509