Poisson Distribution
Poisson Distribution
- calculating randomly scattered events in time or in space
- Examples
- number of road accidents in given period
- goals scored in a soccer match
- number of Losses/Claims occurring in a given period
- number of customers calling in a day
Formula
- In order to apply the Poisson distribution, the various events must be independent.
General formula of Poisson distribution is:
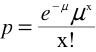 e is the base of natural logarithms (2.7183)
μ is the mean number of "successes"
x is the number of "successes" in question
e is the base of natural logarithms (2.7183)
μ is the mean number of "successes"
x is the number of "successes" in question
Example
Suppose you knew that the mean number of customer calls to your company on a weekday is 8.
- What is the probability that on a given weekday there would be 11 calls?
- This problem can be solved using the following formula based on the Poisson distribution:
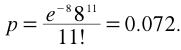 In a spreadsheet
=POISSON(11,8,false)
In a spreadsheet
=POISSON(11,8,false)
since the mean is 8 and the question pertains to 11 calls.
- The mean of the Poisson distribution is μ.
- The variance is also equal to μ.
- Thus, for this example, both the mean and the variance are equal to 8.
Quiz
<quiz display=simple>
{The mean number of defective products produced in a factory in one day is 21. What is the probability that in a given day there are exactly 12 defective products?
|type="{}"} { 0.012 | .012 }
{
Answer >>
0.012
0.012 can be obtained using the formula.
}
{Which of these can be computed using Poisson distribution?
|type="[]"}
-average waiting time between phone calls
+number of people killed accidentally by horse kicks
{Which of these can be computed using Poisson distribution? |type="[]"} +number of enquiries via online form in a month -probability of selecting a person over 2 meter high

