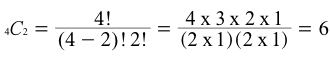Permutations and Combinations
Possible Orders
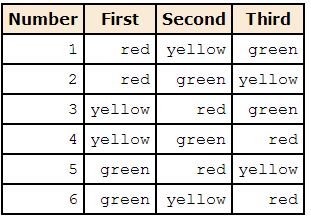
Suppose you had a plate with three pieces of candy on it: one green, on red and one yellow.
- You are going to pick up these three pieces one at a time.
- In how many different orders can you pick up the pieces?
Table below lists all the possible orders.
- There are two orders in which red is first: red, yellow, green and red, green, yellow.
- Similarly, there are two orders in which yellow is first and two orders in which green is first.
- This makes six possible orders in which the pieces can be picked up.
The formula for the number of orders is shown below.
Number of orders = n! where n is the number of pieces to be picked up. The symbol "!" stands for factorial. In a spredsheet =FACT(3)
Some examples are:
3! = 3 x 2 x 1 = 6 4! = 4 x 3 x 2 x 1 = 24 5! = 120
Multiplication Rule (Cartesian Product, Cross Product)
Imagine a small restaurant whose menu has 3 soups, 2 entrées, and 3 desserts. How many possible meals are there?
|
|
Permutations
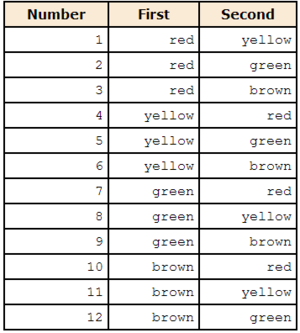
Suppose that there were four pieces of candy (green, red, brown, and yellow).
- You were only going to pick up exactly two pieces.
- How many ways are there of picking up two pieces?
Table below lists all the possibilities.
- The first choice can be any of the four colors.
- For each of these 4 first choices there are 3 second choices.
- Therefore there are 4 x 3 = 12 possibilities.
The number of permutations of four things taken two at a time.
- In other words, it is the number of ways r things can be selected from a group of n things.
- The general formula is:
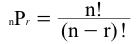where nPr is the number of permutations of n things taken r at a time
In a spreadsheet =PERMUT(4,2)
It is important to note that order counts in permutations.
- That is, choosing red and then yellow is counted separately from choosing yellow and then red.
- Therefore permutations refer to the number of ways of choosing rather than the number of possible outcomes.
- When order of choice is not considered, the formula for combinations is used.
Combinations
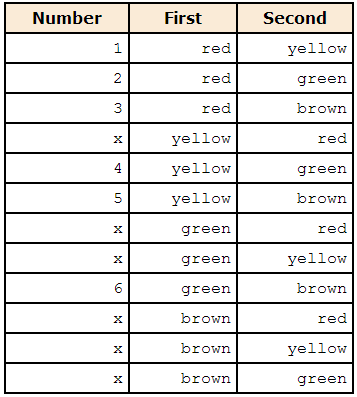
Now suppose that you were not concerned with the way the pieces of candy were chosen but only in the final choices.
- In other words, how many different combinations of two pieces could you end up with?
- In counting combinations, choosing red and then yellow is the same as choosing yellow and then red because in both cases you end up with one red piece and one yellow piece.
- Unlike permutations, order does not count.
- The table below is based on the table above but is modified so that repeated combinations are given an "x" instead of a number.
- For example, "yellow then red" has an "x" because the combination of red and yellow was already included as choice number 1.
- There are six combinations of the three colors.
The formula for the number of combinations is shown below where nCr is the number of combinations for n things taken r at a time.
For our example,
6
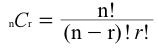
which is consistent with the table above.
Example
Suppose there were six kinds of toppings that one could order for a pizza. How many combinations of exactly 3 toppings could be ordered?
- Here n = 6 since there are 6 toppings and r = 3 since we are taking 3 at a time.
- The formula is then:
In a spreadsheet =COMBIN(6,3)
Quiz
TODO: Create more relevant examples in business situations and more quetsions
