Variance Sum Law II
Variance Sum Law
Recall that when the variables X and Y are independent, the variance of the sum or difference between X and Y can be written as follows:
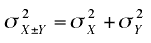which is read: "The variance of X plus or minus Y is equal to the variance of X plus the variance of Y."
When X and Y are correlated, the following formula should be used:
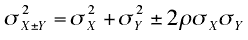where ρ is the correlation between X and Y in the population.
Example
If the variance of verbal SAT were 10,000, the variance of quantitative SAT were 11,000 and the correlation between these two tests were 0.50, then the variance of total SAT (verbal + quantitative) would be:
which is equal to 31,488.
The variance of the difference is:
which is equal to 10,512.
Sample Variance Sum Law
If the variances and the correlation are computed in a sample, then the following notation is used to express the variance sum law:
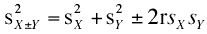
Quiz
<quiz display=simple >
{If the variance of Test A is 100, the variance of Test B is 225, and the correlation between the tests is 0.5, what is the variance of Test A + Test B?
|type="{}"}
{ 475 }
{
Answer >>
475
100 + 225 + (2)(.5)(10)(15) is 475
}
{If the variance of Test A is 100, the variance of Test B is 225, and the correlation between the tests is 0.5, what is the variance of Test A - Test B?
|type="{}"} { 175 }
{
Answer >>
175
100 + 225 - (2)(.5)(10)(15) is 175
}
