R - Regression

Linear regression is an approach to modelling the relationship between a dependent variable y and one or more explanatory variables X.

• One explanatory variable -> simple regression
• Many explanatory variables -> multiple regression
• Multiple correlated dependent y variables are predicted -> multivariate linear regression

Linear regression is usually used for:

• Prediction/forecasting
• Quantify the strength of the relationship between y and the X_j

Implementation:

• Least squares
• Least absolute deviations
• Ridge regression

Regression Model

$y_i={\beta }_1{x}_{i1}+\cdots +{\beta }_p{x}_{ip}+{\epsilon }_i$

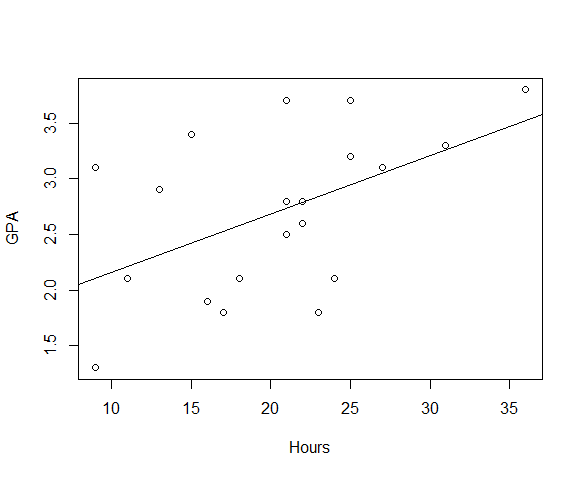
Hours Studying and GPA

"How well does the average number of hours studying predict GPA?"

• Predictor variable - Hours
• Response (criterion) variable - GPA

 # Read the data 
 gpa <- read.table("http://training-course-material.com/images/8/86/Study-time-gpa.txt",h=T)
 
 # Pearson correlation
 cor(gpa)

 # Draw a scatter plot
 plot(gpa)

 # Create a model
 m <- lm(GPA ~ Hours, data=gpa)

 # Show the model
 m

 # Validate the model
 summary(m)

 # Draw the model
 abline(m)

 # What would be a score for studding for 34 hours
 p <- predict.lm(m,data.frame(Hours = c(34)))
 p

Exercises

Using linear regression, find the predicted post-test score for someone with a score of 43 on the pre-test.

http://training-course-material.com/images/8/84/Pre-post-test-scores.txt